În acest articol propun un set de metode de rezolvare pentru algoritmul Time complexity, descris la adresa: https://app.codility.com/programmers/lessons/3-time_complexity/

Un pic de teorie

Este o metodă de a arăta în cât timp se execută un set de operații / calcule asupra unui set de date. Odată cu creșterea valorilor de prelucrat crește în mod liniar și timpul de execuție (linear time). Contant time, îl întâlnim în cazul în care timpul de execuție nu se modifică odată cu creșterea setului de date, iar quadratic time apare în momentul în care timpul de execuție crește (pătratic – n²) odată cu creșterea setului de date.

Time Complexity este exprimat adesea în notație Big O (O()), care indică limita superioară a timpului de execuție în funcție de dimensiunea intrării.

Bog O presupune o metodă de notație a timpului de execuție în care:

• O(n) este folosit pentru linear time
• O(1) este folosit pentru contant time
• O(n²) este folosit pentru quadratic time

În care n este numărul de elemente dintr-un șir.

Logica algoritmului este de a determina tipul timpului de execuție prin determinarea expresiei cu cea mai mare creștere dintr-o ecuație.

Exemplu: a*n+b rezultă că termenul care crește cel mai repede este a*n ceea ce înseamnă că este o funcție liniară O(n).

Dacă am avea o funcție de tipul: a*n²+b*n+v, cea mai rapidă creștere este la a*n² ceea ce înseamnă că este o funcție pătratică.

Un videoclip care explică și demonstrează foarte fain terminologia poate fi vizionat aici: https://www.youtube.com/watch?v=D6xkbGLQesk&ab_channel=CSDojo

Legat de performanțele de execuție în Excel cu referință la câteva tehnici de optimizare puteți găsi explicații detaliate aici: https://learn.microsoft.com/en-us/office/vba/excel/concepts/excel-performance/excel-improving-calculation-performance

Problema FrogJmp

În această problemă se demonstrează un algoritm de tip O(1) în care avem o singură execuție pentru că setul de date este tot timpul la fel (X, Y, D) , în seturile de test fiind diferite doar valorile acestora. În specificații ni se spune că o broască pornește de la poziția 10 presupunem pe o axă 2D. Dacă ea sare pe o distanță (D) de 30 unități, câte sărituri trebuie să facă pentru a ajunge la poziția 85. Ca idee se presupune că broasca nu sare cu virgulă :) ci sunt doar sărituri întregi.

Rezolvarea este destul de simplă în celula C5: avem formula: =ROUNDUP((C2-C1)/C3;0)

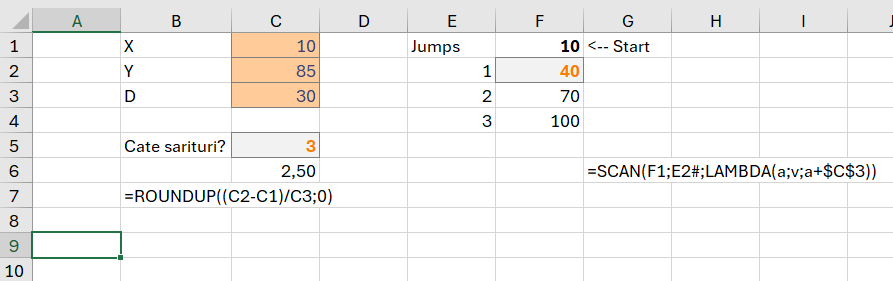
în care funcția ROUNDUP() se folosește pentru rotunjirea în sus a rezultatului obținut. Ca să putem împărți corect distanța de parcurs (D, C3) ar trebui să scădem din destinație (Y, C2) valoarea poziției de start (X, C1).

În partea a doua am realizat un interval cu valori care să specifice unde ajunge broasca la fiecare săritură (jump). Ca să pot realiza dinamic valorile pentru săritură am folosit un scan pe coloana E, în care adun valoare acumulată anterior la valoarea distanței D.

Problema PermMissingElem

Această problemă este din categoria O(n) pentru că numărul de prelucrări depunde de numărul elementelor din șirul propus spre rezolvare.

Problema presupune un șir de numere întregi care ar fi teoretic un șir. Scopul este de a obține numărul elementelor (numerelor lipsă) din intervalul dat.

Se dă șirul {8, 3, 2,  5, 7} în celula A4.

În care:

• celula A7: avem descompunerea șirului cu TEXTSPLIT(), eliminarea spațiilor din șir cu TRIM() și sortare ascendentă cu SORT();
• în B7: calculez valoarea minimă din șir: =MIN(A7#)
• în B8: calculez valoarea maximă din șir: =MAX(A7#)
• în D7: generez secvența completă de la numărul cel mai mic la cel mai mare: =SEQUENCE(C7-B7+1;;B7;1). Numărul de elemente va fi numărul maxim din șir minus numărul minim +1.
• În celula E7 am calculat dacă numărul din secvența completă (D7#) este în secvența propusă. Pentru aceasta folosesc: =IFNA(XMATCH(D7#;A7#);”x”) în care XMATCH() face căutarea între cei doi vectori iari IFNA() pune valoarea X în căsuța numărului lipsă.
• Rezultatul final l-am trecut în celula G7: =TEXTJOIN(„, „;;FILTER(D7#;E7#=”x”; „-„)) în care am unificat toate valorile lipsă din șir prin filtrarea secvenței complete (D7#) pentru care rezultatul căutării este egal cu valoarea „x”. Am folosit TEXTJOIN pentru a unifica rezultatele din FILTER.

Unificate toate coloanele intermediare într-o singură formulă aceasta ar fi:

=LET(arr; SORT(--TRIM(TEXTSPLIT(A4;;",")));
          all; SEQUENCE(MAX(arr)-MIN(arr)+1; ;MIN(arr); 1);
          vCheck; IFNA(XMATCH(all; arr;0 ); "x");

TEXTJOIN(", ";;FILTER(all;vCheck="x"; "-")))

Aplicabilitatea practică a acestui model poate fi destul de interesantă.

Un exemplu ar fi acela în care avem un interval de date și vrem să identificăm dacă lipsește una din ele. Alt exemplu, avem un exemplu de litere (coduri, etc) și dorim să identificăm literele care lipsesc.

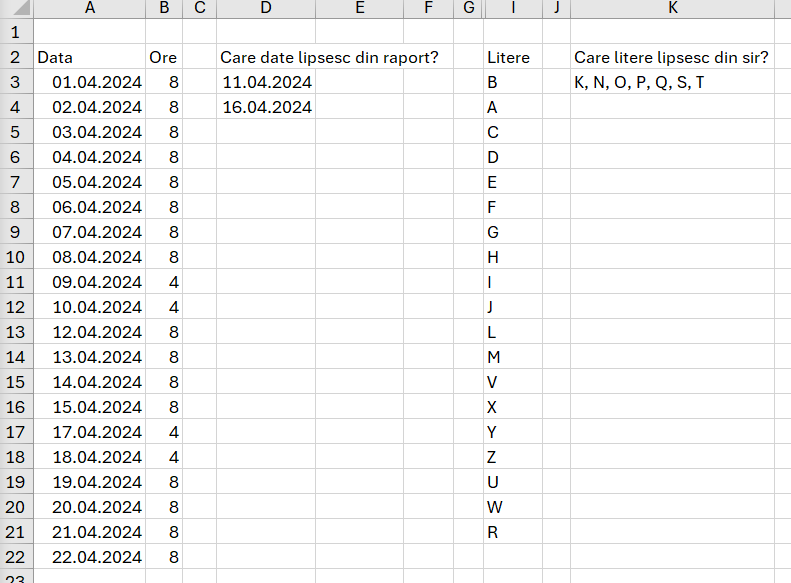
Funcția din D3 este:

=LET(arr; SORT(A3:A22);
          all; SEQUENCE(MAX(arr)-MIN(arr)+1; ;MIN(arr); 1);
          vCheck; IFNA(XMATCH(all; arr;0 ); "x");

FILTER(all;vCheck="x"; "-"))

Funcționarea algoritmului este posibilă datorită faptului că datele în Excel sunt de fapt numere.

În celula K3 am folosit funcția:

=LET(arr; SORT(CODE(I3:I21));
          all; SEQUENCE(MAX(arr)-MIN(arr)+1; ;MIN(arr); 1);
          vCheck; IFNA(XMATCH(all; arr;0 ); "x");

TEXTJOIN(", ";;CHAR(FILTER(all;vCheck="x"; "-"))))

Funcția nu poate lucra la propriu cu litere, de aceea a trebuit să folosesc funcția CODE() în variabila arr pentru a le transforma în coduri ascii. Apoi la final am transformat din coduri ascii în caractere cu funcția CHAR().

Problema TapeEquilibrium

Problema TapeEquilibrium este următoarea: se dă un vector de numere întregi. Vectorul trebuie să împărțit în două sub-șiruri, calculând suma fiecărui sub-șir și găsind diferența absolută dintre sumele lor. Scopul este de a minimiza această diferență absolută.

Algoritmul care rezolvă această problemă are o complexitate de timp O(n), unde n este lungimea vectorului de intrare. Acesta parcurge vectorul o singură dată pentru a calcula suma tuturor elementelor și, apoi, utilizează această sumă pentru a găsi diferența minimă dintre sumele sub-șirurilor.

Într-o abordare simplă problema este foarte ușor de rezolvat:

Se dă șirul {3, 1, 2, 4, 3}. Aflați cea mai mică valoare sau mai bine spus valoarea de echilibru pe șirul de valori.

Pentru rezolvarea simplistă la B2 nu am introdus nici o valoare, apoi am compus suma celor de deasupra până în poziția anterioară minus suma celor rămase. Funcția ABS() transformă numerele negative în pozitive.

Doar că unificarea într-o singură formulă mi-a dat ceva bătăi de cap. Unul din principiile de bază în lucrul, nu numai în Excel, este KISS – Keep It Simple and Stupid.

În prima versiune:

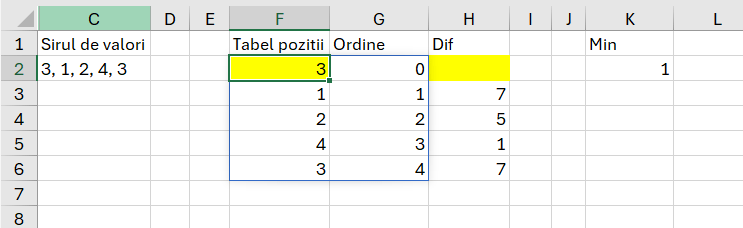
Am creat un tabel intermediar cu numerele și ordinea de la 0.

Apoi am aplicat o ditamai funcția pentru a face diferența. Scopul era de a le unifica într-una singură.

Formula din F2 pentru obținerea tabelului:

=LET(arr; --TRIM(TEXTSPLIT(C2;;", "));
          poz; SEQUENCE(ROWS(arr);;0);
          tabi; HSTACK(arr; poz);
   tabi)

în care arr este lista de numere, poziția este o secvență începând de la 0 iar tabi este variabila pentru a le unifica pe cele două. Scopul era de a traversa tabelul linie cu linie și extragerea valorilor de sus și jos pe baza poziției.

Formula din H2 este cam alambicată:

=LET(arr; F2#;
cc; ROWS(arr);
pc; TAKE(arr;;1);
dc; TAKE(arr;;-1);
BYROW(arr;
LAMBDA(rr;
LET(pv; TAKE(rr;;1);
dv; TAKE(rr;;-1);
pp; TAKE(pc;dv);
dp; TAKE(pc;-(cc-dv));
sum; ABS(SUM(pp)-SUM(dp)); rez; IFERROR(sum;""); rez))))

în care:

• arr – preia tabelul rezultat din funcția anterioatră;
• cc – determină numărul de rânduri al șirului;
• pc – extrage prima coloană din tabelul arr;
• dc – extrage a doua coloană din tabelul arr;
• BYROW() parsează tabelul linie cu linie;
• LAMBDA() face referire la linia curentă prin variabila rr
• În LET() definesc un alt set de variabile pentru valorile de pe linie: pv (prima valoare), dv, valoarea de pe coloana 2, pp este prima parte din prima coloana din pozitia curenta (dv)-1, dp este a doua parte a primei coloane, apoi determin suma primei părți (pp) cu a doua parte (dp).

Iese dar la unificarea celor două funcții obțin niște rezultate dubioase, în loc de 7, 5, 1, 7 obțin 2, 1, 1, 0 ceea ce înseamnă că undeva fac o greșeală. Cu cât este mai complexă abordarea cu atât este mai greu de controlat rezultatul intermediar.

Așa că am ales o abordare diferită și am ales să folosesc funcția INDEX în mod dinamic în detrimentul funcției TAKE din varianta anterioară:

Minusul acestei rezolvări este că nu pot folosi o variabilă de descompunere direct în LET() ci trebuie să refer un set de celule deja transformate în valori.

Primul pas a fost descompunerea șirului în celula A7 cu: =–TRIM(TEXTSPLIT(A2;;”,”))

Funcția din D2 care îmi calculează valoarea minimă este:

=LET(arr; A7#; poz; SEQUENCE(ROWS(arr));
pp; MAP(poz; LAMBDA(v; SUM(INDEX(arr;1):INDEX(arr;v))));
dp; MAP(poz; LAMBDA(v; IFERROR(SUM(INDEX(arr;v+1):INDEX(arr;ROWS(arr)));"")));
diff; IFERROR(ABS(pp-dp);""); MIN(diff))

în care:

• arr – preia vectorul rezultat din split;
• poz – determină șirul de valori de lungimea vectorului, începând cu 1 de această dată (implicit);
• pp – preia valorile din prima parte a lui arr prin declararea variabilei v în LAMBDA în așa fel încât să construiesc un idex dinamic de la poziția 1 la poziția v curent în care v este poziția curentă din pozițe;
• dp – a doua parte preia în același stil cu INDEX() valorile de la poziția curentă a lui v de pe secvență până la finalul lui arr ROWS(arr).
• diff – calculează diferența absolută dintre cele două numere rezultate din însumare.

Ca să pot face depanare în această funcție mi-am făcut un tabel de rezultate intermediare, utilizând o combinație de HSTACK cu VSTACK.

vCheck; HSTACK(VSTACK("Sirul"; arr);VSTACK("Pozitia"; poz);VSTACK("Partea de sus"; pp);VSTACK("Partea de jos"; dp); VSTACK("Diferenta"; diff));

Un exemplu de problemă din viața reală unde algoritmul TapeEquilibrium ar putea fi util este în domeniul financiar, în special în gestionarea portofoliilor de investiții.

Să presupunem că aveți un portofoliu de investiții format din acțiuni și alte active financiare. Diferitele active pot fluctua în valoare în timp, iar obiectivul dumneavoastră este să gestionați aceste fluctuații și să minimizați riscul. O abordare comună este să împărțiți portofoliul în două părți și să încercați să mențineți echilibrul între ele.

Algoritmul TapeEquilibrium ar putea fi utilizat pentru a determina cea mai bună modalitate de a distribui activele între cele două părți ale portofoliului într-un mod echilibrat, astfel încât să se minimizeze riscul general. Calculând diferența absolută între sumele valorilor active din cele două părți, puteți ajusta distribuția pentru a obține o diferență minimă și, implicit, un portofoliu mai stabil și mai echilibrat din punct de vedere financiar.

Cam asta este pentru astăzi. Dacă ceva este greșit vă rog să nu ezitați să-mi scrieți în comentarii.

Sper să fie util cuiva!