Continui seria de articole despre algoritmii clasici din programare cu o metodă de rezolvare a problemelor de căutare descrise în articolul de pe Codility: https://app.codility.com/programmers/lessons/14-binary_search_algorithm/
Ar trebui să specificăm de la începutul articolului că metodele de rezolvare propuse nu sunt poate cele mai optime din punct de vedere al vitezei de procesare, dar sunt un mod interesant de a demonstra că Excelul este mult mai mult decât A1+B2 și fiecare dintre utilizatorii de Excel pot găsi funcții și formule interesante pe care să le aplice în diverse domenii și operații pe care le efectuează în activitatea lor.
Dacă sunteți doar în căutarea unor funcții de căutare, vă reamintesc un articol mai vechi Funcția Filter() din #Excel 365 în care sunt descrise comparativ mai multe funcții de căutare din Excel.
În articolul curent forța Excelului este demonstrată prin funcțiile MAKEARRAY() și SCAN() într-o construcție specială. Veți vedea.
Nu avem numaidecât o parte de teorie în afara algoritmului descris la începutul articolului. Ambele probleme în schimb mi-au dat destul de multă bătaie de cap cu înțelegerea cerințelor. Cred că aici este de fapt dificultatea lor.
Problema MinMaxDivision
Această problemă este orientată pentru a determina care este minimul sumei unor numere din poziții consecutive dintr-un vector, dacă îl împarți în K părți de diferite dimensiuni. Un aspect ciudat al problemei este că vectorul poate fi împărțit în elemente vide. De exemplu dacă ai un vector de 7 elemente și un K de 3 poți împărți vectorul în 3 segmente de 7, 0, 0. Suma tuturor numerelor din vectorul de 7 este suma maximă care poate fi atinsă. Scopul este să îl împarți în segmente a căror sumă maximă să fie cea mai mică din toate formele de a împărți elementele.
În problemă este introdus și termenul M care reprezintă de fapt dimensiunea maximă a valorilor din vectorul A. Această valoare M trebuie să fie mai mică decât minimul de maximum combinații.
Propunerea de rezolvare
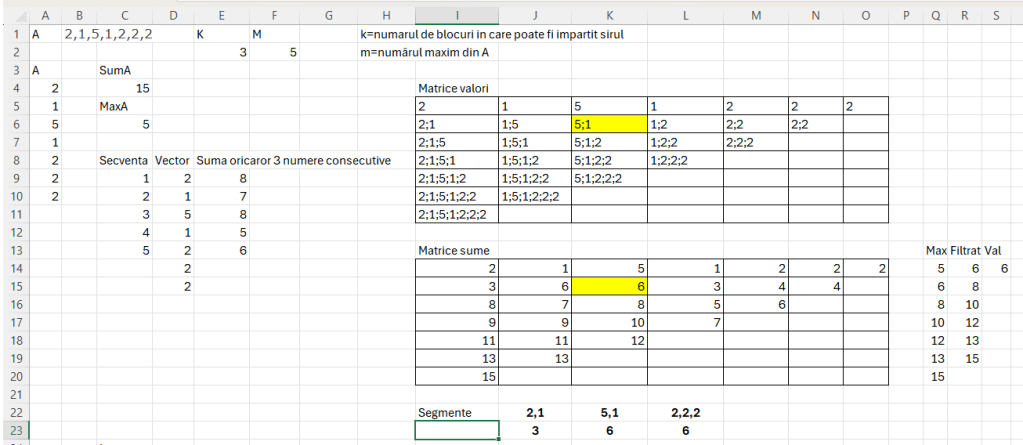
În primă fază a rezolvării problemei nu am înțeles numaidecât că numărul K reprezintă numărul de segmente în care se poate împărți șirul și am ralizat un calcul de însumare a tuturor combinațiilor de numerele consecutive în E9.
Funcția din E9: =MAP(C9#;LAMBDA(v;SUM(INDEX(D9#;SEQUENCE(3;;v)))))
în care în MAP() refer secvența de numere generate pe dimensiunea vectorului -2. Valoarea de -2 este pentru a preveni erorile în funcție datorate indexării în afara vectorului. În acest fel ultima poziție de indexare v este dimensiunea vectorului -2 ceea ce înseamnă că valoarea 3 din Sequence() de final va face indexarea până la finalul vectorului D9#.
Pentru cei mai puțin familiarizați cu funcțiile dinamice un index() poate aduce mai multe elemente dintr-un vector dacă specificăm acest lucru prin SEQUENCE(3) sau ROW(1:3) de exemplu. Eu prefer SEQUENCE pentru că poți specifica valori dinamice, pe când ROW() nu funcționează cu variabile.
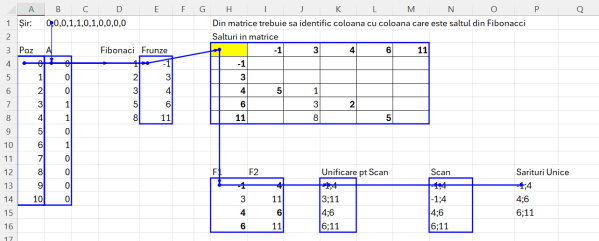
Pentru a înțelege toate combinațiile posibile am generat o matrice în I5 în care indexez lista de elemente consecutive în ordinea lui r: câte unul, câte două, câte 3… și așa mai departe. Formula din I5 este:
=MAKEARRAY(ROWS(A4#);ROWS(A4#);LAMBDA(r;c;IFERROR(TEXTJOIN(";";TRUE;INDEX(D9#;SEQUENCE(r;;c)));"")))în care pentru a putea aduce și afișa valorile din vectorul D9# folosesc funcția TEXTJOIN(). Magic în această formulă este indexul de secvență de r valori începând de la coloana c.
A fost destul de dificil să ajung la această abstractizare. Ulterior în I14 am înlocuit TEXTJOIN() cu SUM() de indexare dinamică pentru a calcula valorile fiecărui segment.
În Q14 am utilizat funcția =MAX(I14:O14) pentru a determina maximul pe fiecare linie, după care în R14 am filtrat doar valorile mai mari decât M, obținând apoi prin MIN() valoarea 7.
Integrați toți acești pași dau următoarea formulă:
=LET(sir; --TEXTSPLIT(B1;;",");
_k;E2; _m; F2; _rs; ROWS(sir);
matrix; MAKEARRAY(_rs;_rs;LAMBDA(r;c;IFERROR(SUM(INDEX(sir;SEQUENCE(r;;c)));"")));
_maxs; BYROW(matrix;MAX);
return; MIN(FILTER(_maxs; _maxs>_m));
return)Frumos în această formulă este variabila _maxs care aplică noua formă de utilizare a BYROW() în cadrul tabelelor fără a folosi separat o LAMBDA() care ar complica problema.
Exemplu practic: Alocarea unui buget de investiții
O companie are un buget total de investiții pe care trebuie să-l împartă între mai multe proiecte. Problema constă în împărțirea optimă a bugetului astfel încât suma maximă alocată unui singur proiect să fie cât mai mică posibil.
Datele problemei:
Ai N proiecte de investiții (echivalentul secțiunilor dintr-un șir de numere).
Fiecare proiect necesită o anumită sumă de bani (vectorul A din problemă).
Ai K departamente (echivalentul lui K din problemă), iar fiecare departament trebuie să gestioneze un set de proiecte.
Scopul este să împarți proiectele între cele K departamente astfel încât suma maximă alocată unui singur departament să fie minimizată.
Exemplu numeric:
Să presupunem că avem 5 proiecte care necesită următoarele sume de bani (în milioane):
A = [2, 1, 5, 1, 2, 2, 2]
Și trebuie să le alocăm la K = 3 departamente.
Obiectiv: Împărțirea optimă astfel încât suma maximă cheltuită de un singur departament să fie minimizată.
Posibile împărțiri
O posibilă împărțire ar fi:
[2, 1, 5] | [1, 2] | [2, 2]
Sumele alocate fiecărui departament: 8, 3, 4
Maximul este 8 (prima grupă).
O altă împărțire mai echilibrată:
[2, 1] | [5, 1] | [2, 2, 2]
Sumele alocate: 3, 6, 6
Maximul este 6 – mai echilibrat decât primul caz.
Problema NailingPlanks
În această problemă este vorba despre optimizarea numărului de cuie (C) care pot fi folosite pentru fixarea unui set de scânduri A-B.
Ca orice problemă de optimizare și aceasta este destul de dificilă de abordat pentru că avem foarte multe excepții. De exemplu cuiul din poziția 4 poate fișa și scândura 1 cât și scândura 2, ceea ce înseamnă că nu mai are sens să folosim cuiul din poziția 2 care poate fixa doar scândura 1. Cu ajutorul cuielor 6 și 7 putem fixa scândura 3, deci nu are sens să îl folosim pe al doilea.
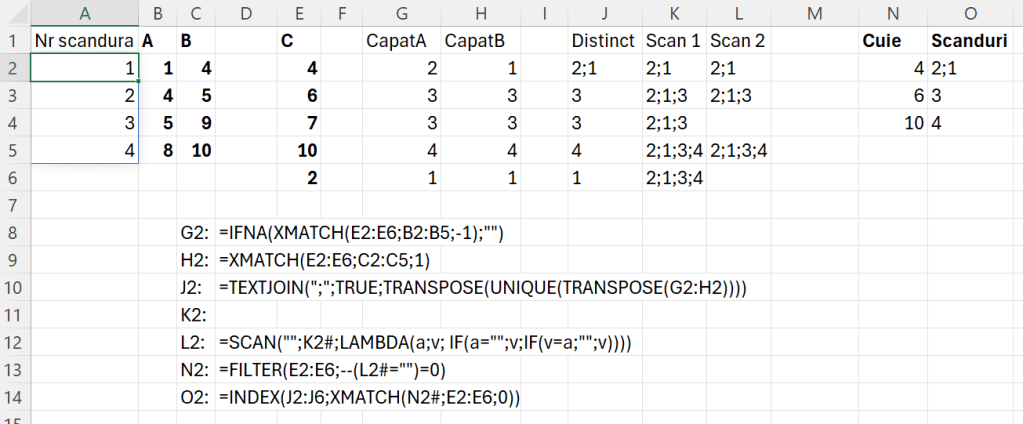
În rezolvarea problemei am căutat în G2 și H2 în ce interval de valori din A și B se află valoarea poziției cuiului. îmn XMATCH() am folosit parametrul -1 (egal sau mai mic decât valoarea căutată) pentru capătul de jos al scândurii (A) iar pentru capăt B am folosit parametrul 1 (egal sau mai mare decât valoarea căutată). Acesta este artificiul de căutare în intervale de numere prin XMATCH()
Ca să văd dacă un cui fixează mai multe scânduri în J2 am făcut o concatenare de numere unice. Rezultatul prelucrării anterioare fiind de tipul unui vector pe linie, ca să pot aplica funcția UNIQUE(), trebuie transpozate numerele rezultat, funcția de unicitate funcționează doar la nivel de vectori în coloană. Al doilea TRANSPOSE() nu este numaidecât obligatoriu atât timp cât folosesc TEXTJOIN() dar pentru a vedea rezultatele pe parcurs atunci l-am utilizat.
Partea cea mai dificilă dincolo de G2 și H2 a fost să determin care scândură a fost inserată cu un cui și să o elimin din rezultat. Pentru asta am abordat cu SCAN() în K2. Formula din K2 este:
=SCAN(0;J2:J6;LAMBDA(a;v; IF(a=0; v;
LET(_a; TEXTSPLIT(a; ";");
_v; TEXTSPLIT(v; ";");
ver; IFNA(XMATCH(_v;_a;0);0);
fil; TEXTJOIN(";";TRUE;FILTER(_v;ver=0;""));
TEXTJOIN(";";TRUE;a;fil)))))Ca să pot prelucra și compara numerele în variabila ver, a trebuit să descompun întâi valorile acumulatorului a și a valorii curente v. Dacă nici una din valorile curente nu se găsesc în ce a fost anterior, facem join între valoarea curentă și cea acumulată. Dacă valorile sunt deja în șir atunci aducem doar valoarea existentă.
Această formulă este foarte utilă pentru a putea compara șiruri de numere între ele și a acumula doar numărul care nu a mai fost. Exemplificare de extragere a tuturor valorilor unice dintr-un vector de valori
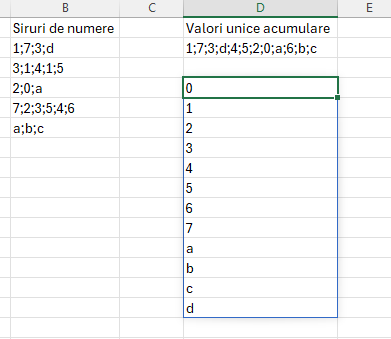
Funcția REDUCE() din D2 imi aduce doar rezultatul final al unui SCAN() fără a mai fi necesară trecerea prin fiecare etapă. Funcția din D2 este identică cu cea prezentată anterior doar că în loc de SCAN am folosit Reduce. Pentru a determina valorile în ordinea lor în D4 am introdus formula: =SORT(TEXTSPLIT(D2;;”;”))
Aceasta este cea mai de valoroasă funcție din acest articol, după opinia mea.
Revenind la problema inițială, în celula L2 am introdus o nouă funcție de scanare pentru a determina valorile unice din Scan 1 în poziția lor inițială. Apoi pentru a determina poziția cuielor am folosit Filtrarea în N2 apoi indexarea în O2 pentru a afla scândurile fixate de acele cuie.
Aparent complicat, dar soluționabil. Ar trebui testate pentru mai multe seturi de valori pentru îmbunătățirea soluției.
Pentru integrarea funcție trebuie avut în vedere că folosesc un Textjoin care nu funcționează într-un Byrow pentru construcția variabilei Dist, deci trebuie construită o funcție recursivă (fReqDist) anterioară. În final formula ar fi:
=LET(_a; B2:B5; _b; C2:C5; _c; E2:E6;
CapatA; IFNA(XMATCH(_c;_a;-1);"");
CapatB; IFNA(XMATCH(_c;_b;1);"");
fReqDist; LAMBDA(v; TEXTJOIN(";";TRUE;(UNIQUE(TRANSPOSE(v)))));
tabi; HSTACK(CapatA; CapatB);
Dist; BYROW(tabi; LAMBDA(r; fReqDist(r)));
Scan1; SCAN(0;Dist;LAMBDA(a;v; IF(a=0; v;
LET(_a; TEXTSPLIT(a; ";");
_v; TEXTSPLIT(v; ";");
ver; IFNA(XMATCH(_v;_a;0);0);
fil; TEXTJOIN(";";TRUE;FILTER(_v;ver=0;""));
TEXTJOIN(";";TRUE;a;fil)))));
Scan2; SCAN("";Scan1;LAMBDA(a;v; IF(a="";v;IF(v=a;"";v))));
Cuie; FILTER(_c;--(Scan2="")=0);
Scanduri; INDEX(Dist;XMATCH(Cuie;_c;0));
Result; HSTACK(Cuie;Scanduri);
Result
)Având în vedere complexitatea problemei sunt și cazuri pe care soluția oferită nu oferă răspunsul optim. Exemplificare:
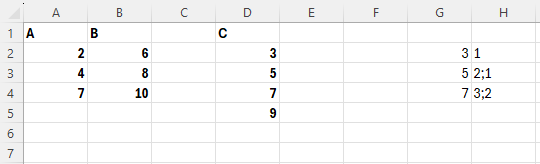
În această problemă optimul ar fi două cuie… poziția 5 și 7 sau 5 și 9, dar rezolvarea propusă anterior are o mică problemă cu scan-ul pentru prima valoare. Mi-ar plăcea să văd dacă un cititor poate să-mi trimită o soluție mai corectă pentru cazurile particulare.
Cam atât pentru astăzi.
Sper să fie util cuiva!