Am revenit cu o propunere de rezolvare în Excel, din seria algoritmilor clasici. Doar nu credeați că am renunțat! :) Scuze dacă mai scriu greșit anumite cuvinte sau virgule… din viteză pentru a nu pierde idea. Dacă aveți observații sau comentarii, rog folosiți secțiunea dedicată.
În acest articol voi propune diferite metode de rezolvare a problemelor din categoria algoritmilor Prefix Sums, cunoscuți și sub numele de Scan, Cumulative Sum sau Inclusive Scan, se referă la o serie de metode eficiente pentru calcularea sumelor prefixelor unei secvențe de numere. Prefixul unei secvențe este definit ca suma elementelor din secvență până la un anumit punct.
Algoritmii Prefix Sums sunt utilizați frecvent în diverse domenii ale informaticii, cum ar fi:
- Procesare secvențială: Algoritmii Prefix Sums pot fi utilizați pentru a calcula rapid sumele prefixelor unei secvențe de numere, ceea ce este util pentru diverse operații de procesare secvențială, cum ar fi căutarea binară, intervale de sume, și detectarea de elemente repetitive.
- Baze de date: Algoritmii Prefix Sums pot fi utilizați pentru a implementa eficient indexuri de rang, care permit determinarea rapidă a numărului de elemente dintr-o secvență care sunt mai mici sau egale cu o anumită valoare.
- Algoritmi de căutare: Algoritmii Prefix Sums pot fi utilizați pentru a accelera algoritmii de căutare, cum ar fi căutarea binară, prin precalcularea sumelor prefixelor.
Principiul de bază:
Ideea centrală a algoritmilor Prefix Sums este de a stoca o secvență suplimentară de numere numită „prefix sum array”. Această secvență conține suma elementelor din secvența originală până la un anumit punct. De exemplu, dacă secvența originală este [1, 2, 3, 4, 5], atunci prefix sum array-ul ar fi [1, 3, 6, 10, 15].
Odată ce prefix sum array-ul este calculat, se pot calcula sumele prefixelor oricărui interval din secvența originală cu o singură operație de scădere. De exemplu, pentru a calcula suma elementelor de la indicele 2 la indicele 4 (inclusiv), se calculează prefix sum array[4] – prefix sum array[1] = 15 – 3 = 12.
În Excel există o serie de funcții care ne ajută să implementăm nativ algoritmul, doar că problemele expuse sunt mai complexe pentru a putea fi rezolvate doar cu funcția SCAN().

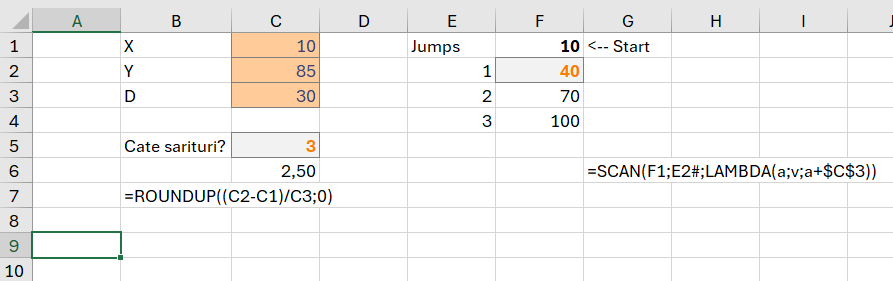
În imagine este prezentat un exemplu prin care putem utiliza funcția SCAN pentru a determina suma elementelor de pe un array cu SCAN() sau suma tuturor elementelor dintr-un vector. Există mai multe metode și funcții pe care le putem utiliza pentru a aduce date de la o poziție la altă poziție a unui vector: OFFSET(), DROP(), INDEX().
În funcția =SCAN(0;A2:A9;LAMBDA(a;v;a+v)) scanăm vectorul A2:A9 și aplicăm funcția LAMBDA() în care avem parametrii a – acumulator și v – value (cu referire la valoarea de pe linia curentă). În acest exemplu adunăm cele două valori, pe linia următoare, a va aduna la suma de pana acum suma valorii curente (v).
În același fel funcționează și REDUCE() doar că în loc să calculeze pentru fiecare valoare a vectorului, aplică funcția fiecărui element din vector.
Ca să putem elabora un vector dinamic pentru prefix sums avem nevoie de o poziție de start și de final din șir. În celulele D4, E4, F4, G4 am prezentat diferite funcții care pornesc de la același start și au același număr de celule de extras (3). Diferența între funcții este că Offset() pornește de la 0 în abordarea unui bloc de celule la fel cu DROP().
În continuare voi propune diferite metode de rezolvare în Excel a problemelor de pe site-ul https://app.codility.com/programmers/lessons/5-prefix_sums/
Problema PassingCars
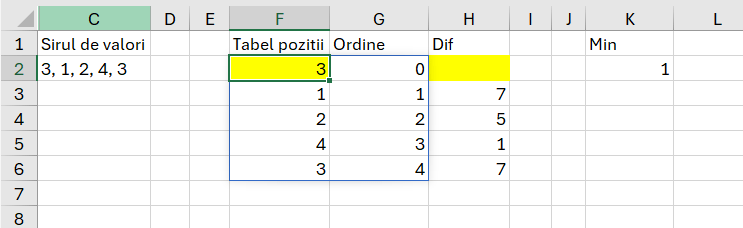
Problema PassingCars este o problemă clasică de algoritmică care se referă la calcularea numărului de perechi de mașini care se depășesc reciproc pe o șosea cu o singură bandă. Mașinile se deplasează în ambele direcții și pot depăși alte mașini mai lente. Problema constă în determinarea numărului de perechi de mașini care se depășesc reciproc într-un anumit interval de timp sau pe o anumită porțiune de drum.
![Problema PassingCars ]n Excel](https://valygreavu.com/wp-content/uploads/2024/05/image-11.png?w=1024)
În propunerea de rezolvare, ca să înțeleg modul de abordare al problemei în vederea determinării numărului de perechi, am dus șirul în 2D F2xG1 după care am aplicat o combinație de funcții (I3) pentru a calcula minimul între linii și coloane. În funcție există un hardcode (7 de la numărul coloanei și 2 de la numărul de linii) dar este și problema că returnează și o combinație eronată, perechea 1-2 care nu este corectă.
În zona F9 – M14 am schimbat modul de implementare, transformând șirul în direcția Est (G10) prin splitarea șirului din B2. Apoi în coloana Start (F10) determin o secvență de numere de la 0 pe baza numărului de linii a vectorului G10#. Pentru a reprezenta ordinea mașinilor dinspre Vest (H10) ca să le pot compara cu cele care vin din Est am folosit sortarea descendentă (-1) a valorilor de pe Est (G10#) după cele de pe Start (F10). Pentru a determina punctul final am inversat șirul start prin sortarea descendentă (-1). Conform cerințelor problemei, ne interesează când mașinile care vin din Est ( valoarea 0) se intersectează cu cele care vin din Vest (valoarea 1). Ca să pot realiza acest lucru a trebuit să fac o filtrare a valorilor de pe coloana Start cu cele de pe coloana Est. Din cauza faptului că șirul de Start începe de la 0 iar eu intenționez să folosesc funcția de căutare INDEX() a trebuit să adaug valoarea 1 funcției din J9: =TRANSPOSE(FILTER(F10#;G10#=0)+1). Această transpozare a valorilor rezultat mă ajută să determin ceea ce se întâmplă în zona J10.
Funcția din J10 generează numărul de perechi pentru primul 0 din direcția Est. Apoi pe K10 aplic aceeași funcție.
=IF(INDEX(G10#;J9)=0;IF(H10#=1;IF(INDEX(F10#;J9)<I10#;INDEX(F10#;J9)&”-„&I10#;””);””);””)

Problema acestei metode de implementare este dată de faptul că dacă aș avea mai mulți de 0 în șirul original, atunci ar trebui să copii manual formula în dreapta. Pentru a expune perechile unice în ordinea lor folosesc în M10 o combinație de TOCOL() cu UNIQUE() și SORT() apoi număr aceste valori în Q10.
Treaba oarecum mai dificilă a fost să integrez toate aceste coloane și formule de comparație într-o singură funcție complet dinamică. Am ajuns cu greu la rezultat, din aproape în aproape.
=LET(est;--TEXTSPLIT(B2;;",");
start;SEQUENCE(ROWS(est);;0);
vest;SORTBY(est;start;-1);
final;SORT(start;;-1);
fRecursive; LAMBDA(x;y;FILTER(x;y=0));
cols; fRecursive(start; est)+1;
tabi;IFNA(HSTACK(start;est;vest;final;cols);"");
tabperechi; MAKEARRAY(ROWS(est); ROWS(cols);
LAMBDA(r;c; IF(INDEX(est;INDEX(cols; c))=0;
IF((INDEX(vest; r))=1;
IF(INDEX(start;INDEX(cols; c))<INDEX(final; r);
INDEX(start;INDEX(cols; c))&"-"&INDEX(final; r);"");"");"")));
peru; LET(s; SORT(UNIQUE(TOCOL(tabperechi;1))); FILTER(s; s<>""));
nr; ROWS(peru);
IFNA(HSTACK(VSTACK("Perechi: ";peru); VSTACK("Nr: "; nr)); ""))Primele variabile sunt echivalentul din explicațiile anterioare. Prima provocare a fost să determin valorile echivalente din J9, valori care se regăsesc în variabila cols. Doar că nu pentru a putea calcula această variabilă aveam nevoie de o funcție Lambda() recursivă definită în variabila fRecursive. Această funcție o folosesc pentru a face filtrarea valorii echivalente pozițiilor 0 din șirul spre Est. fRecursive doar definește ce să facă funcția mai jos și care sunt parametrii. Ca să pot vedea rezultatele intermediare am creat un tabel în variabila tabi care adună coloană cu coloană variabilele definite anterior. IFNA() în folosesc în acest context pentru a elimina erorile NA determinate de faptul că numărul de elemente a lui cols poate fi mai mic decât numărul de elemente a șirului.
Rezultatul până la tabi este:

Marea provocare a apărut la procedura de calculare a perechilor pe datele din tabi. Ca să pot determina perechile de mașini după algoritmul explicat pentru celula J10, a trebuit să revin la funcția MAKEARRAY() pentru ca calcula o matrice dinamică cu numărul de linii exchivalent numărului de elemente ale șirului și numărul de coloane echivalent numărului de 0 întâlnit. Rezultatul intermediar din variabila tabperechi este:

Apoi în variabila peru am determinat perechile unice, în variabila nr am determinat numărul lor, după care am făcut o combinație de HSTACK cu VSTACK pentru a genera un tabel dinamic, cu tot cu capul de tabel.
Dincolo de aplicabilitatea în monitorizarea traficului auto, PassingCars poate fi adaptat în domeniul economic pentru:
- Analiza cererii și ofertei pe piețele bursiere – Numărarea de câte ori o ofertă de cumpărare satisface o cerere de vânzare sau invers.
- Gestionarea stocurilor – Monitorizarea cererilor de produse într-un depozit și numărarea momentelor în care sosirile de stocuri (oferte) satisfac cererile.
- Fluxul de aprovizionare într-o fabrică – Cererile pentru piese specifice și momentele în care acestea sunt furnizate.
Problema CountDiv
Este o problemă clasică de algoritmică care se referă la calcularea numărului de divizori ai unui număr dat într-un interval specificat. De exemplu, dacă intervalul este [a, b] și numărul dat este n, problema solicită determinarea numărului de divizori ai lui n care se află în intervalul [a, b].
Exemplu: Considerați intervalul [1, 10] și numărul dat 20. Divizorii lui 20 în acest interval sunt 1, 2, 4, 5 și 10. Prin urmare, numărul de divizori ai lui 20 în intervalul [1, 10] este 5.
În analiza de date, se poate folosi pentru a număra evenimente periodice într-un interval de timp. De exemplu, dacă avem date despre evenimente care se întâmplă la fiecare 10 zile și vrem să știm câte astfel de evenimente au avut loc într-o anumită perioadă de timp.
Exemplu: Dacă avem evenimente la fiecare 10 zile și dorim să știm câte evenimente au avut loc între ziua 15 și ziua 95.
A = 15, B = 95, K = 10

Pentru a afla numărul de evenimente care se întâmplă într-o lună (A 1 – start, B 31 final) odată la 4 zile (K 4) trebuie să caclulăm întregul împărțirii lui B la K apoi întregul împărțirii lui A-1 la K după care facem diferența între rezultate.
Dacă dorim să aflăm zilele din calendar pentru care trebuie să programăm acele acțiuni, am propus în G2 formula:
=SEQUENCE(;E4;IF(B3>=B1;B3;IF(MOD(B1;B3)=0;B1;B1+(B3-MOD(B1;B3))));B3)
pentru generare a unei secvențe de numere pornind de la numărul de divizori (E4) în secvențe de câte K (B3). Apoi în pentur a determina numărul de la care se pornește trebuie să fac un calcul comparativ între A și K:
- Daca K>=A atunci primul divizor devine K;
- Daca K<A atunci :
- daca restul impartirii lui A la K = 0 (MOD(A;K) atunci primul divizor este A;
- daca nu sunt divizibile atunci formula de calcul al primului divizor din interval devine A + (K – MOD(A; K))
Condiția principală este ca A să fie mai mare ca B.
Ca să pot folosi într-o singură funcție personalizată, același algoritm poate fi implementat într-o funcție lambda care se poate salva în Name manager (Ctrl+F3). Funcția propusă ar fi:
=LAMBDA(A;B;K;SEQUENCE(;INT(B/K)-INT((A-1)/K);IF(K>=A;K;IF(MOD(A;K)=0;A;A+(K-MOD(A;K))));K))(B1;B2;B3)
în care B1, B2, B3 sunt celulele de testare pentru funcție. În această lambda putem identifica mai bine algoritmul de calcul explicat în pseudocod anterior.
În gestiunea stocurilor, algoritmul poate fi folosit pentru a determina câte reaprovizionări au avut loc într-un anumit interval de timp. De exemplu, dacă un produs trebuie reaprovizionat la fiecare 7 zile, putem calcula câte reaprovizionări au avut loc într-un interval de timp specificat. Alt exemplu din producție, dacă un echipament necesită mentenanță la fiecare 30 de zile și dorim să știm câte sesiuni de mentenanță au avut loc între ziua 50 și ziua 200.
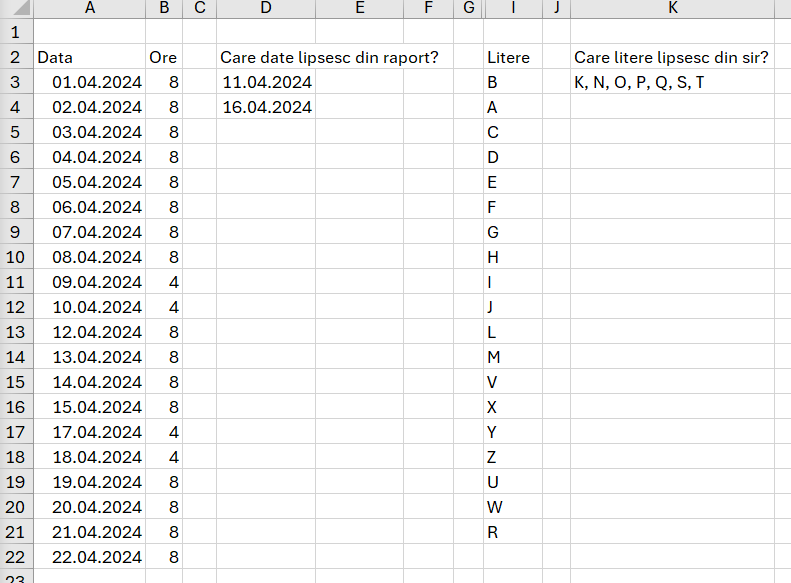
Problema GenomicRangeQuery
Algoritmul GenomicRangeQuery este utilizat pentru a găsi factorul minim de impact al nucleotidelor într-o anumită secvență de ADN, în intervalele specificate. Avem o secvență de ADN reprezentată de un șir de caractere care conține literele A, C, G și T. Aceste litere au factorii de impact corespunzători: A = 1, C = 2, G = 3, T = 4. Trebuie să răspundem la mai multe interogări de tip interval, unde pentru fiecare interogare, ni se cere să găsim factorul minim de impact al nucleotidelor într-un sub-interval al secvenței de ADN. Un șir de caractere S reprezentând secvența de ADN. Două array-uri P și Q de aceeași lungime, unde fiecare pereche (P[i], Q[i]) definește un interval [P[i], Q[i]] în șirul S. Pentru fiecare interogare (P[i], Q[i]), se va returna minimul factorilor de impact al nucleotidelor din intervalul [P[i], Q[i]].
În contextul geneticii, termenul „factor de impact al nucleotidelor” nu este unul uzual. Însă, în multe probleme algoritmice, acest termen se referă la o reprezentare numerică simplificată pentru a evalua rapid o secvență genetică. Totuși, dacă ne referim la interpretarea nucleotidelor și la impactul lor în biologie, putem discuta despre semnificația biologică a diferitelor nucleotide (baze ADN: adenina (A), citozina (C), guanina (G), timina (T)) și cum anumite secvențe pot afecta funcționarea genelor.
Propunerea de rezolvare în Excel presupune descompunerea șirurilor de intrare, așezarea lor pe diferite celule și metode de extragere și funcții de căutare.

Intrările în model sunt ADN, S – secvența P și Q cele două perechi din secvență pe care le căutăm. A9, D3, H3, I3 sunt funcții de descompunere a textului pe linii. în J3 folosesc o metodă cu OFFSET(). Cei care au mai lucrat în trecut cu el, au permanent tendința de a se duce spre zona de vectori dinamici sprea această funcție. Doar că mie mi-a spus odată un expert în Excel că funcțiile de acest tip sunt funcții volatile și nu se recomandă a se utiliza. Și totuși, le folosesc de câte ori am nevoie și nu găsesc altă soluție mai rapidă. DROP() este un pic mai complex pentru că trebuie să extragi un segment din vector, pozițiile de deasupra și de dedesupt.
Rezolvarea în descompuneri în diferite zone și funcții de căutare este destul de simplă în Excel. Problema este când încerci să le unifici… pentru că sunt prea mulți vectori de parcurs în cadrul aceleeași operații. Vă prezint în continuare funcția din B15. Nu sunt extraordinar de mândru pentru că m-am chinuit prea mult… iar eu am în Excel un principiu: Dacă te muncești prea mult ca să faci un lucru, înseamnă că ceva nu faci bine.
=LET(vtab;
LET(pa;B3;qa;B4;
fRecursive;LAMBDA(p;q;
LET(vP;--TEXTSPLIT(p;;",");
vQ;--TEXTSPLIT(q;;",");
vPQ;HSTACK(vP;vQ);
vRows; BYROW(vPQ;LAMBDA(r;TAKE(r;;-1)-TAKE(r;;1)+1));
vStart;vP+1;
HSTACK(vStart;vRows)));
fRecursive(pa;qa));
vCod;MID(B1;SEQUENCE(LEN(B1));1);
vPoz;SEQUENCE(LEN(B1));
vADN;MID(B2;SEQUENCE(LEN(B2));1);
vvADN;XLOOKUP(vADN;vCod;vPoz;9999);
ac;MAX(CHOOSECOLS(vtab;2));
ar;ROWS(CHOOSECOLS(vtab;1));
tabfin;MAKEARRAY(ar;ac;
LAMBDA(r;c;
LET(pv;INDEX(vtab;r;1);
dv;INDEX(vtab;r;2);
MIN(INDEX(vvADN;SEQUENCE(dv;;pv))))));
valfin;BYROW(tabfin;LAMBDA(r;MIN(r)));
valfin)Marea problemă a fost să pot face un tabel intermediar cu valorile de start în căutare și lungimea segmentului care va trebui extras. Cele două coloane din imaginea de mai jos, echivalentul variabilei vtab pe care o definesc în LET cu ajutorul funcției recursive care se numește fRecursive.

Uneori când sunt prea mulți vectori de parcurs, atunci segmentăm funcția în rezultate intermediare prin intermediul altor funcții LET() dar în care de multe ori definim astfel de funcții recursive. Funcțiile recursive pot fi definite și extern în Name manager (Ctrl+F3).
Cheia în funcția fRrecursive din definirea vtab este obținerea lungimii șirului de extragere (cea de-a doua coloană). Pentru a face această operațiune am folosit variabila vRows care prin BYROW() calculează diferența dintre coloanele P și Q (funcțiile TAKE) la care adaugă valoarea 1, pentru că în parcurgerea vectorilor din Excel cu funcții INDEX() de cele mai multe ori pornim de la valoarea 1.
Ulterior după ce a fost definit tabelul vtab folosim maximul din a doua coloană în variabila ac și numărul de linii rezultat în variabila ar. Aceste două variabile le folosim mai jos în variabila tabfin în care creem un tabel de ac coloane și ar linii pentru care aplicăm lambda care ne ajută la indexarea valorilor din segmentul ADN stocate în variabila vvADN.

valfin este ultima variabilă prin care BYROW() calculează minimul de pe fiecare linie.
Cel mai greu în rezolvare am ajuns la cele două valori coloane din vtab.
Analiza pieței de acțiuni
Dincolo de această problemă, algoritmul se poate aplica în domeniul economic pentru a ajuta la decizia de a investi sau nu într-un pachet de acțiuni. Se dă un șir de prețuri zilnice ale unei acțiuni și vrei să găsești prețul minim dintr-un anumit interval de zile pentru a lua decizii de investiții.
Variabilele de intrare:
- S (prețuri acțiuni): Un șir de prețuri zilnice ale acțiunilor.
- P și Q (intervale de interogare): Două liste care conțin perechi de început și sfârșit pentru fiecare interval de zile în care vrei să analizezi prețul minim.
S = [23, 29, 21, 32, 25, 28, 24] (prețurile zilnice ale acțiunii)
P = [1, 2, 4] (începutul intervalelor de interogare)
Q = [3, 5, 6] (sfârșitul intervalelor de interogare)
Explicația lui P și Q.
Intervalul 1: de la ziua 1 la ziua 3
Intervalul 2: de la ziua 2 la ziua 5
Intervalul 3: de la ziua 4 la ziua 6

Pentru a calcula prețurile minime trebuie să știm că nu mai avem din funcția anterioară variabilele specifice pentru vADN si vvADN. Noua funcție care este derivată din cea anterioară este:
=LET(
vtab;LET(pa;B35;qa;B36;
fRecursive;LAMBDA(p;q;
LET(vP;--TEXTSPLIT(p;;",");
vQ;--TEXTSPLIT(q;;",");
vPQ;HSTACK(vP;vQ);
vRows;BYROW(vPQ;LAMBDA(r;TAKE(r;;-1)-TAKE(r;;1)+1));
vStart;vP+1;
HSTACK(vStart;vRows)));
fRecursive(pa;qa));
vvADN;--TEXTSPLIT(B34;;",");
ac;MAX(CHOOSECOLS(vtab;2));
ar;ROWS(CHOOSECOLS(vtab;1));
tabfin;MAKEARRAY(ar;ac;
LAMBDA(r;c;LET(pv;INDEX(vtab;r;1);
dv;INDEX(vtab;r;2);
MIN(INDEX(vvADN;SEQUENCE(dv;;pv))))));
valfin;BYROW(tabfin;LAMBDA(r;MIN(r)));
valfin)Dincolo de dificultatea de implementare în Excel, GenomicRangeQuery este un algoritm foarte important de umrărit pentru că poate aplica (dincolo de minim) orice funcție asupra unor intervale de date definite ceea ce poate permite rezolvarea unor probleme de complexitate oarecum mai ridicată.
Problema MinAvgTwoSlice
Algoritmul MinAvgTwoSlice este o soluție la o problemă de găsire a unei subsecvențe continue de dimensiune minimă (de cel puțin două elemente) într-un șir de numere întregi, astfel încât media aritmetică a acestei subsecvențe să fie cât mai mică posibil. Problema este oarecum asemănătoare cu GenomicRangeQuery doar că de data aceasta trebuie să calculăm media aritmetică pe toate intervalele posibile, nu doar pe câteva intervale specificate.
Propunere de rezolvare

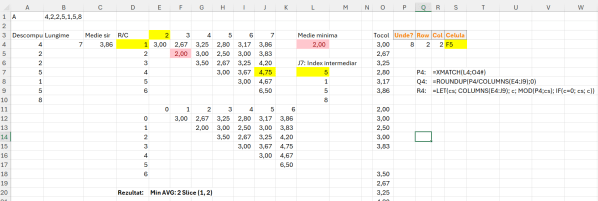
În rezolvarea problemei prin descompuneri, ca să pot face un tabel de căutare din două dimensiuni specifice lungimii șirului A, am introdus în E3 funcția: =SEQUENCE(;B4-1;2) în care în B4 avem lungimea șirului, -1 ca să pot avea același număr de elemente pornid de la 2. Aceste valori le folosesc pentru a specifica faptul că în algoritm nu pot porni de la 1:1 ci de la 1:2. La D4 am folosit funcția =SEQUENCE(B4-1) cu start de la 1 (nespecificat) dar ca să aibă același număr de elemente cu numărul de coloane. Folosesc -1 pentru că un șir intermediar nu poate porni de la ultima poziție a sa, cerința algoritmului fiind să ne raportăm la minim două elemente. In E4 am introdus apoi funcția de medie dinamică pe baza indexării liniilor cu coloanele. =IF($D4>=E$3;””;AVERAGE(INDEX($A$4#;$D4):INDEX($A$4#;E$3))). Rezultatul intermediar care ar apărea în J7 înainte de a face media este prezentat în imagine. Ca să pot afla apoi celula unde se află aceasă valoare minimă, am utilizat în S4 o funcție pe care o dezvoltasem mai demult pentru căutarea adresei unei celule dintr-un tabel pe baza unei valori specificate. Rezultatele intermediare pentru această funcție sunt specificate în P4, Q4 și R4.
=LET(aria; E4:J9;
ca; MIN(COLUMN(aria))-1;
ra; MIN(ROW(aria))-1;
tc; TOCOL(aria;1);
unde; MATCH(L4;tc;0);
col; LET(cs; COLUMNS(aria);
c; MOD(unde;cs);
IF(c=0; cs; c))+ca;
row;ROUNDUP(unde/COLUMNS(aria);0)+ra;
cel; CHAR(64+col)&(row);
cel)Trebuie menționat că limită a acestei funcții că ea funcționează doar pentru tabele de date poziționate în sectorul de coloane A:Z.
Variabila aria conține tabelul de date pe care dorim să-l analizăm pentru a căuta valoarea pe care am obținut-o în celula L4. Acolo este trecută valoarea de căutare, stocată în variabila unde. Variabila unde scanează valoarea din L4 pe coloana obținută din aducerea la o dimensiune a tabelului aria. Ca să determin coloana din foaia de calcul în care se află valoarea folosesc un let care calculează poziția celulei în aria la care adună valoarea variabilei ca, care reprezintă numărul coloanei din foaia de calcul la care începe aria. Valoarea rezultat este stocată în variabila col. Aceeași procedură un pic simplificată este și la determinarea valorii variabilei row care este o rotunjire în sus (ROUNDUP) a locului unde se află valoarea în vectorul pe coloană împărțit la nnumărul de coloane al ariei, la care se adaugă valoarea variabilei ra care calculează linia la care începe aria în foaia de calcul. Ulterior calculez variabila cel prin care determin caracterul alfabetic de la A la Z. Litera A are codul 65 de aceea încep de la 64 în CHAR().
Pentru a întoarce rezultatul din E20 care include media minima și slice echivalent în poziții din șir folosesc următoarea funcție:
=LET(sir;A4#;
vLen;ROWS(sir);
tab; MAKEARRAY(vLen;vLen;
LAMBDA(r;c;IF(r>=c;"";AVERAGE(INDEX(A4#;r):INDEX(A4#;c)))));
vmin; MIN(tab);
tc; TOCOL(tab);
unde; XMATCH(vmin; tc;0);
vRow; ROUNDUP(unde/COLUMNS(tab);0);
vCol; LET(cs; COLUMNS(tab); c; MOD(unde;cs); IF(c=0; cs; c));
"Min AVG: "&vmin&" Slice ("&vRow-1&", "&vCol-1&")"
)Reprezentarea variabilei tab este în imaginea de la soluția problemei în aria E12:K18. Celelalte variabile sunt rezultate intermediare explicate în problemă.
În economie acest algoritm ar putea fi utilizat în analiza costurilor de producție. De exemplu într-o fabrică se înregistrează costurile zilnice de producție. Un manager ar putea încerca să identifice media cea mai mică pe cel mai mic interval de zile, unde costurile au fost cele mai mic. În felul acesta poate corela cu alte date pentru a identifica ce s-a făcut diferit pentru a obține costuri mai scăzute.
Exemplu de problemă pentru un șir de date:

Cam asta a fost pentru acest articol. Multă treabă mai este…
Sper să fie util cuiva!