Modele de algoritmi în #Excel – Prime and composite numbers (10)

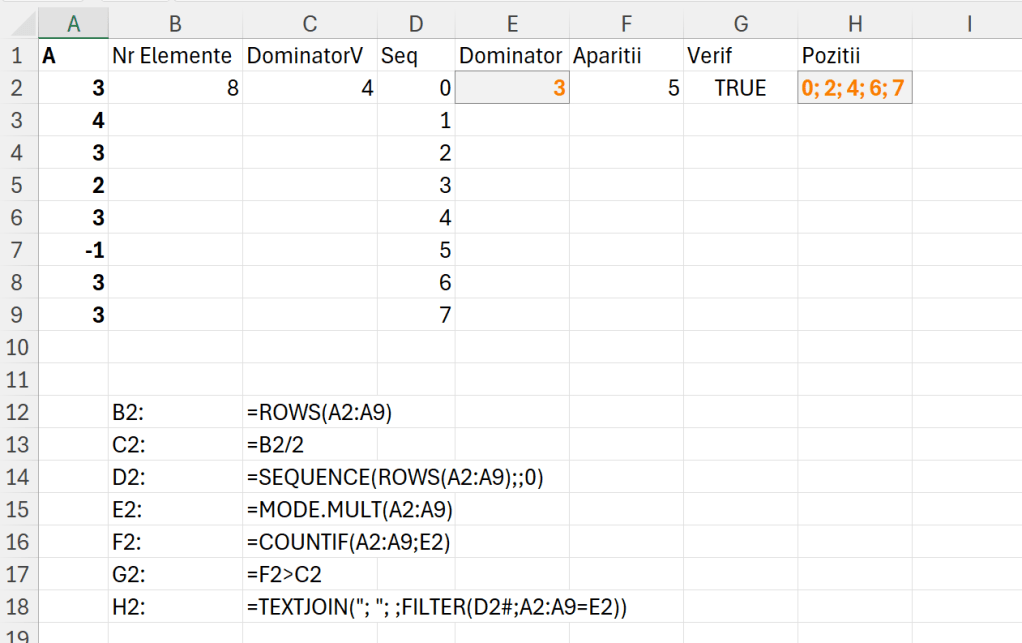
Dacă nu v-a plăcut niciodată matematica, mai bine nu citiți acest articol. Vă fac eu un rezumat: E nasol! :)

Dar e foarte fain și provocator pentru matematicieni și cei cărora le place să lucreze cu numere. În același timp, dincolo de programare propun o metodă de rezolvare nouă a problemelor de determinare a numerelor prime, desigur cu limitările aferente Excelului care poate face operații cu numere de până la 15 cifre sau în care numărul de linii este limitat la 1048576 adică 2 la puterea 20.

Prezentul articol propune o metodă de rezolvare a problemelor de pe site-ul Codility și le găsiți în detaliu la adresa: https://app.codility.com/programmers/lessons/10-prime_and_composite_numbers/

Fiind vorba de mai multă matematică să începem cu…

Puțină teorie

Un număr natural 𝑛 > 1 este numit prim dacă are exact două divizori pozitivi: 1 și n. Exemple: 2, 3, 5, 7, 11 etc. Un număr natural 𝑛 > 1 care nu este prim este numit compus. Acesta are mai mult de doi divizori. Exemple: 4, 6, 8, 9, 12 etc.

Fără a intra în prea multe detalii matematice, verificarea dacă un număr este prim are la bază testul lui Fermat care a fost extins de către matematicianul James Grime la metoda AKS, care are o probabilitate mai mare de soluții corecte. În matematica aplicată în criptografie, cea mai cunoscută metodă de determinare a unui număr prim este cunoscută sub denumirea de Miller-Rabin. Metoda este foarte complexă și presupune tehnica de ridicare la puterea numărului analizat, ceea ce în Excel este limitativ. Aplicand testul N maxim poate fi 46 care nu este numar prim. La urmatorul numar, 47, 2^46 rezulta un numar complex de 15 cifre cu care Excelul nu mai poate lucra. Nici formula Willans nu ne ajuta pentru ca avem o componenta de factorial care ne duce la numere mari la aceeasi limitare.

În metoda de rezolvare propusă de mine, am utilizat tehnica de a genera o secvență de numere de la 1 la N după care pe secvență am determinat dacă numărul N împărțit la valoarea curentă este un număr întreg sau zecimal. Voi detalia în secțiunea următoare. Doar că această tehnică a generării de secvențe de numere este costisitoare ca timp de execuție și limitată la N de pana la 2^20, echivalentul numărului de linii din Excel. În căutarea unei metode de optimizare am ajuns la algoritmul Prim-Dijkstra care presupune, în mod simplificat, calcularea radicalului din N, după care verificarea factorilor ramasi de la 2 până la valoare radical. Tehnica aceasta îmi permite să analizez dacă un număr este prim sau nu până la valoarea 1.099.511.627.776 echivalentului lui 2 la puterea 40, un număr de 13 cifre cu care poate lucra Excel. Limitarea este data de faptul că nu pot genera secvențe mai mari de 2^20 care este radicalul lui 2^40.

Exemplificare implementare algoritm Prim-Dijkstra

Implementare și testare algoritm Prim-Dijkstra în Excel.

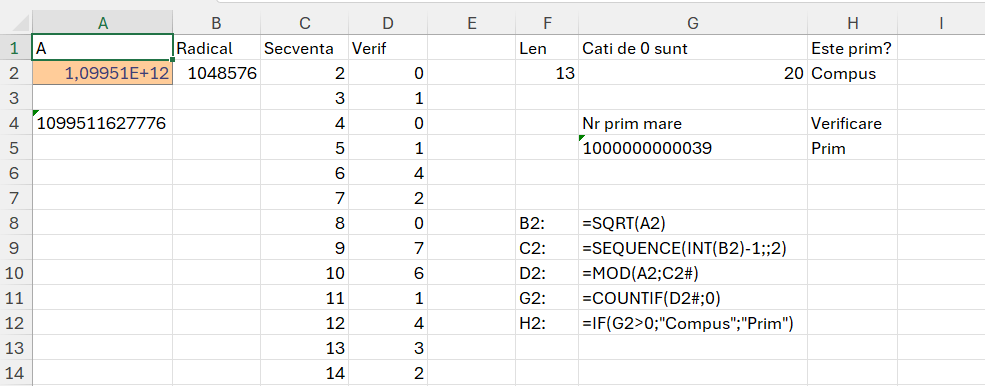
În cazul numerelor prime 2 și 3 modelul prezentat returnează eroare din cauză că nu se poate genera secvența pentru că radicalul este mai mic decât 2. În cazul acesta pentru a rezolva problema lui 2 și 3 funcțiile din C2 și D2 trebuie tratate cu un IFERROR().

Funcția unificată este destul de simplă și are la bază funcțiile prezentate în imagine:

=LET(a;--G5; 
     radical;SQRT(a);
     sec;SEQUENCE(INT(radical)-1;;2);
     unmod;IFERROR(a/sec-INT(a/sec);1);
     TAKE(IF(FILTER(unmod;unmod=0;"x")="x"; 
                    "Prim";
                    "Compus");1;1))

în care variabila unmod este cea care-mi determină în mod diferite față de funcția MOD() prezentată anterior, valoarea 0 sau un număr zecimal, în funcție dacă numărul N se împarte la numărul curent de le secvența din variabila sec.

În încheierea acestei secțiuni, Excelul dispune de un set destul de mare de funcții matematice pe care le putem utiliza în diferite contexte. Pentru mine una din cele mai utile este funcția MOD() explicată și în articolul Modele de algoritmi in #Excel – Vectori (2.1). Apoi mai folosesc MROUND() pentru a rotunji zecimalele la un set de intervale predefinite, un înlocuitor mai nou al funcției CEILING(). De asemenea, folosesc destul de des funcțiile de randomizare și cele de rotunjire. SEQUENCE() care este tot o funcție matematică o utilizez foarte des în locul FOR-ului din programarea clasică și mai folosesc adeseore ISODD sau ISEVEN pentru a determina dacă am un număr par sau impar într-o zona a unei funcții. Interesantă de studiat și prezentat, când o fi timp, funcția AGGREGATE.

În continuarea articolului propun câteva metode de rezolvare a problemelor cu numere prime în Excel.

Problema CountFactors

Dat fiind un număr întreg pozitiv N, problema cere să identificăm numărul total de divizori ai acestui număr, adică numărul de factori pozitivi care împart N exact fără a lăsa rest. Pe scurt k este un divizor al lui N dacă restul împărțirii lui N la k este zero.

În cazul acestei probleme nu putem aplica algoritmul Prim-Dijkstra pentru că ne trebuie toți divizorii. De exemplu dacă ne referim la numărul 24, radical din 24 = 4,89 ceea ce înseamnă că nu luăm în calcul valoarea 6, 8, 12 care sunt divizori ai lui 24. Pentru optimizare am putea sa inmultim fiecare din divizorii sub radical intre ei pentru a determina in oglinda divizorii urmatori.

Rezolvarea problemei pas cu pas:

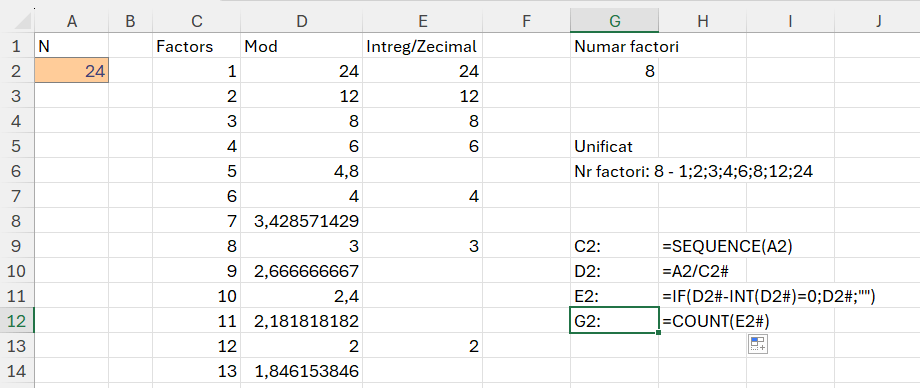
În cazul numerelor prime vom obține doar două valori: 1 și N. Funcția unificată din G6 este:

=LET(_n;A2;
      factors;SEQUENCE(_n);
      mods; MAP(factors;LAMBDA(v;_n/v));
      rezfactors; IF(mods-INT(mods)=0;mods;"");
  "Nr factori: "& COUNT(rezfactors)&" - "&TEXTJOIN(";";TRUE;SORT(rezfactors)))

În care în variabila mods am împărțit numărul _n la valoarea corentă de pe secvența factors. În partea de rezultat am realizat o concatenare ca să includ și factorii.

Funcția lucrează destul de repede pentru numere până la 2^20-1 acest număr (1.048.575) având 48 de factori.

Aplicații practice

Criptografie: Factorizarea numerelor mari este esențială pentru algoritmii de criptare.
Teoria numerelor: Analiza proprietăților numerelor în baza divizibilității.
Probleme de optimizare: Factorii unui număr pot fi utilizați pentru a găsi soluții optime în anumite probleme de împărțire sau combinatorică.

Problema MinPerimeterRectangle

Problema MinPerimeterRectangle se încadrează în categoria problemelor legate de factorizarea numerelor și geometrie elementară.
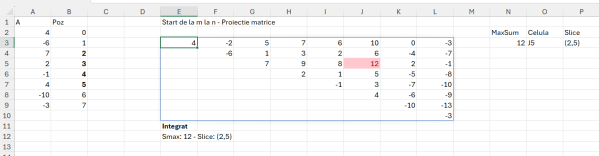
Cerința este să identificăm dreptunghiul cu cel mai mic perimetru care poate fi format folosind divizorii unui număr întreg pozitiv N. Un dreptunghi este format din laturile a și b care satisfac relația: a×b=N. Perimetrul acestui dreptunghi este dat de formula: P=2×(a+b). În mod evident, pentru a minimiza perimetrul, diferența dintre a și b ar trebui să fie cât mai mică posibil, adică a și b ar trebui să fie cât mai apropiate între ele.

Pentru a găsi perechea (a,b) optimă, putem parcurge toți divizorii a ai lui N, apoi calculăm b=N/a. Calculăm perimetrul pentru fiecare astfel de pereche și reținem perimetrul minim.

Propunerea de rezolvare este un pic mai complicată în Excel.

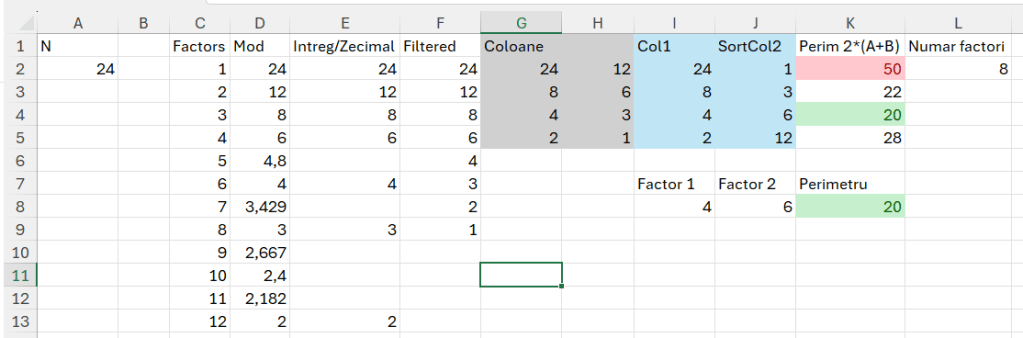
MinPerimeterRectangle rezolvare în Excel

Până la E2 este problema cunoscută prezentată anterior. Ca să pot înmulți numerele între ele, trevuie să le transpun pe două coloane. Doar că în cazul în care numărul de factori ai lui N este un număr impar vom obține în zona G:H o eroare și tot algoritmul nu mai funcționează corect. De aceea, prezint formula direct mai complicată pentru a genera tabelul Coloane (G2:H5):

=LET(filtered;F2#;
     rr;ROWS(filtered);
     IF(ISEVEN(rr);WRAPROWS(filtered;2);
           HSTACK(TAKE(filtered;INT(rr/2)+1);TAKE(filtered;-INT(rr/2)-1))
))

în care verific dacă numărul de linii este un număr par și dacă da împart filtrarea fin F2# la două coloane. WRAPROWS împarte un vector în linii a câte n coloane specificate ca parametrul 2 din exemplul nostru. Numărul de linii variază în funcție de dimensiunea vectorului.

Ca să putem în continuare să facem înmulțirea trebuie să sortăm a doua coloană ascendent. Pentru asta în I2 am folosit funcția: =TAKE(G2#;;1) pentru a prelua prima coloana din tabelul Coloane, as-is iar in J2 am folosit funcția: =SORT(TAKE(G2#;;-1)) pentru a sorta ascendent a doua coloană din tabelul din G2#. Calcularea perimetrului este apoi destul de simplă: =2*(I2#+J2#) iar prin formatare condiționată am formatat cu verde cea mai mică valoare, corespondetă laturilor factori 4, 6. Este demonstrată în acest fel ipoteza din introducere în care cei mai apropiați factori determină cel mai mic perimetru.

Funcția integrată pentru a determina direct factorii si perimetrul cel mai mic, este:

=LET(_n;A2;
      factors;SEQUENCE(_n);
      mods;MAP(factors;LAMBDA(v;_n/v));
      rezfactors;IF(mods-INT(mods)=0;mods;"");
      filtered;FILTER(rezfactors;ISNUMBER(rezfactors));
      rr; ROWS(filtered);
      coloane; IF(ISEVEN(rr); WRAPROWS(filtered;2);
               HSTACK(TAKE(filtered;INT(rr/2)+1);TAKE(filtered;-INT(rr/2)-1)));
      _col1; TAKE(coloane;;1);
      _col2; SORT(TAKE(coloane;;-1));
      tabf; HSTACK(_col1;_col2; 2*(_col1+_col2));
      perimmin; FILTER(tabf; TAKE(tabf;;-1)=MIN(TAKE(tabf;;-1)));
   perimmin
)

în care identificăm explicațiile anterioare dar sub formă de variabile iar la final avem un FILTER() pe minimum de perimetru.

Aplicații practice

Optimizarea costurilor: În construcții, reducerea perimetrului poate însemna reducerea costurilor de material pentru garduri sau borduri, având o anumită arie dată.
Design de produse: În industrie, minimizarea perimetrului unui dreptunghi poate fi importantă pentru ambalaje sau alte produse, unde materialul folosit pentru margini trebuie să fie minimizat.
Logistică: În depozitare și ambalare, calcularea cutiei sau ambalajului cu perimetrul minim pentru o anumită suprafață (de exemplu, etichete) poate reduce consumul de material și costuri.

Problema Flags

Problema Flags este o problemă clasică de optimizare, care presupune plasarea unui număr maxim de steaguri pe vârfurile unei secvențe montane, respectând anumite condiții.

Dată fiind o listă de înălțimi reprezentate printr-un vector A, fiecare element din vector reprezintă înălțimea unui vârf sau a unei depresiuni dintr-un peisaj montan. Un vârf este definit ca o poziție i pentru care: A[i−1]A[i+1]. Distanța dintre două steaguri consecutive să fie de cel puțin K unități, unde K este numărul total de steaguri.

Propunere de rezolvare.

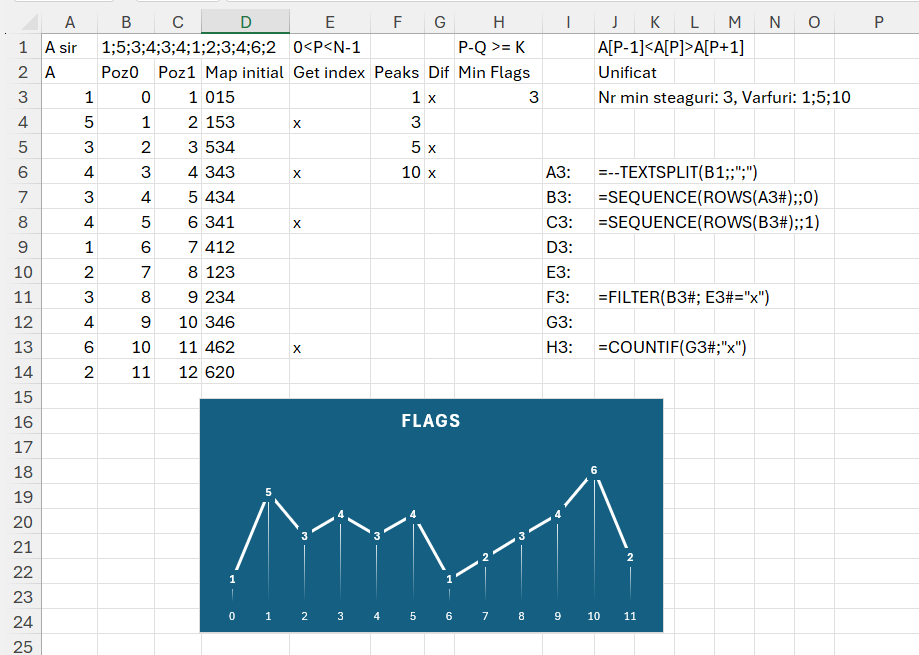
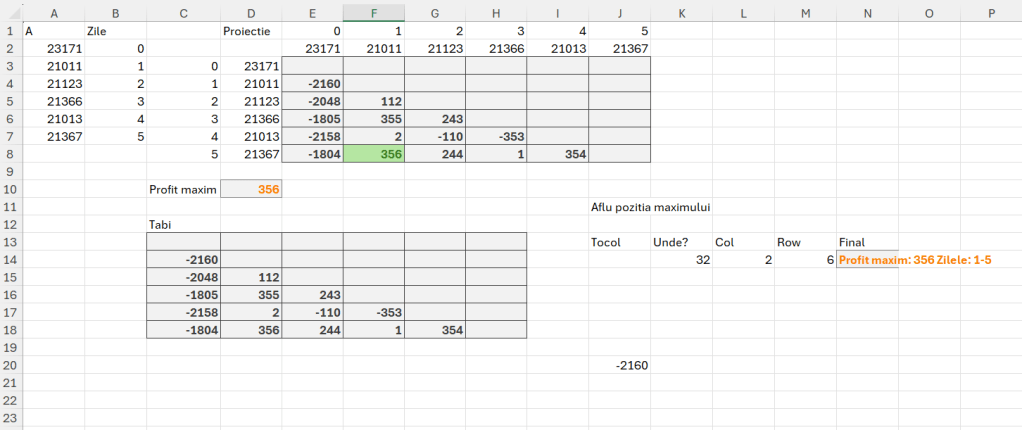
În B2 avem șirul de numere care reprezintă vârful. Șirul este transformat în vector în A3. Inspirat de cei de la Codility am realizat și eu graficul din valoarea vârfurilor. Din câte observăm avem vârfuri în poziția (pornind de la 0) 1, 3, 5, 10. Doar că problema Flags are această chichiță că steagurile trebuie să fie la dimensiune de cel puțin numărul lor între ele. Am identificat că sunt 4 steaguri inițial. Diferența între poziția steagului 1 și 3 nu este de 4, ceea ce înseamnă că steagul 3 cade. Asta este cerința… eu aș fi făcut că dacă sunt două vârfuri consecutive egale punem un singur steag.

În D3 doar am vrut să testez indexarea. Mă gândeam la început să folosesc metoda matricei de triplete, dar nu are sens pentru că nu comparăm toate vârfurile între ele cu doar poziția curentă cu cea anterioară și următoare. În E3 marchez de fapt cu valoarea x valorile care îndeplinesc condiția de vârf. Funcția completă pentru marcare este:

=MAP(C3#; LAMBDA(v; LET(a; A3#; 
                        _p_1; IF(v=1; 0; INDEX(a; v-1)); 
                        _p; INDEX(a;v); 
                        _p_2; IFERROR(INDEX(a; v+1);0); 
           IF(AND(_p_1<_p;_p >_p_2); "x"; ""))))

în care prin funcția MAP parcurg vectorul C3# iar pentru fiecare valoarea v din acesta calculez valoarea variabilelor _p_1, _p și _p_2 pentru a extrage de pe vectorul A3# valoarile și a le compara în IF-ul de la final. Dacă ele îndeplinesc condiția cerută de problemă, atunci marcăm cu x.

În F3 filtrez valorile poziției pe format vector (start de la 0). O mică bătaie de cap o avem în G3 pentru a determina optimul de steaguri prin diferență între poziția lor și numărul lor. Funcția din G3 este:

=LET(peaks;F3#;
     seq;SEQUENCE(ROWS(peaks));
     MAP(seq; LAMBDA(v;IF(v=1;"x";
                          IF(ABS(INDEX(peaks;v)-INDEX(peaks;v-1))>=ROWS(peaks);"x";
                                IF(v-2<1;"";
                                  IF(ABS(INDEX(peaks;v)-INDEX(peaks;v-2))>=ROWS(peaks);"x";"")))))))

în care scanez cu MAP() secvența rezultată din numărul de vârfuri inițial, în cazul nostru 4, după care pentru fiecare valoare calculez diferența absolută între termeni iar dacă aceasta este mai mare decât numărul de vârfuri inițial, marchez cu x. După cum observăm din rezultat rămân marcate vârfurile 1, 5 și 10, ceea ce determină un număr optim de 3 steaguri pe care le putem amplasa pe traseul montan.

Toată povestea aceasta unificată este prezentată în funcția următoare:

=LET( a; TEXTSPLIT(B1;;";");
    _poz0; SEQUENCE(ROWS(a);;0);
    _poz1; SEQUENCE(ROWS(a);;1);
    gindex; MAP(_poz1; LAMBDA(v; LET(_p_1; IF(v=1;0;INDEX(a;v-1));
                                     _p; INDEX(a;v);
                                     _p_2; IFERROR(INDEX(a;v+1);0);
                                     IF(AND(_p_1<_p;_p>_p_2);"x";""))));
    rezfin; FILTER(_poz0;gindex="x");
    minflags; LET(peaks;rezfin;
                  seq;SEQUENCE(ROWS(peaks));
                  MAP(seq; LAMBDA(v;IF(v=1;"x"; 
                           IF(ABS(INDEX(peaks;v)-INDEX(peaks;v-1))>=ROWS(peaks);"x";
                           IF(v-2<1;"";IF(ABS(INDEX(peaks;v)-INDEX(peaks;v-2))>=ROWS(peaks);"x";"")
                     ))))));
ver; IFNA(HSTACK(a;_poz0;_poz1;gindex;rezfin;minflags);""); 
pozminflag; FILTER(rezfin;minflags="x");
fin; "Nr min steaguri: "&COUNT(pozminflag)&", Varfuri: "&TEXTJOIN(";";TRUE;pozminflag); 
fin)

în care putem identifica valorile obținute în coloanele prezentate în imagine, totul cu un singur input: B1, șirul de valori. Având în vedere numărul de pași pe care trebuie să-i parcurgem până la rezultatul final, o tehnică pe care o utilizez este aceea de verificare pe parcurs. Asta o fac cu un HSTACK (variabila ver) în care acumulez rând pe rând coloanele pe care le obțin anterior. IFNA în folosesc pentru cazul în care numărul de linii de la o coloana la alta este diferit.

Aplicații practice

Managementul resurselor: În industria minieră sau forestieră, optimizarea plasării resurselor (cum ar fi sonde sau senzori) poate urma o abordare similară, unde distanța minimă între resurse trebuie respectată.
Planificarea rețelelor: În telecomunicații, plasarea antenelor sau a altor echipamente trebuie să respecte anumite distanțe minime pentru a evita interferențele.
Logistica: În planificarea transporturilor sau a depozitelor, problema poate fi utilizată pentru a optimiza plasarea punctelor de control sau a stațiilor de verificare.

Problema Peaks

Aparent o variantă a problemei Flags, doar că nu mai avem limitarea k de distanță în amplasarea unor steaguri. Avem însă o cerință nouă care solicită împărțirea vectorului care reprezintă un sector montan în segmente egale ca dimensiune. Mai mult de atât fiecare segment trebuie să aibă un vârf. Cerința este foarte faină și are din nou legătură cu optimizarea din practică spre zone din economie în special finanțe și producție. Dozarea efortului ar fi în sinteză.

Propunere de rezolvare:

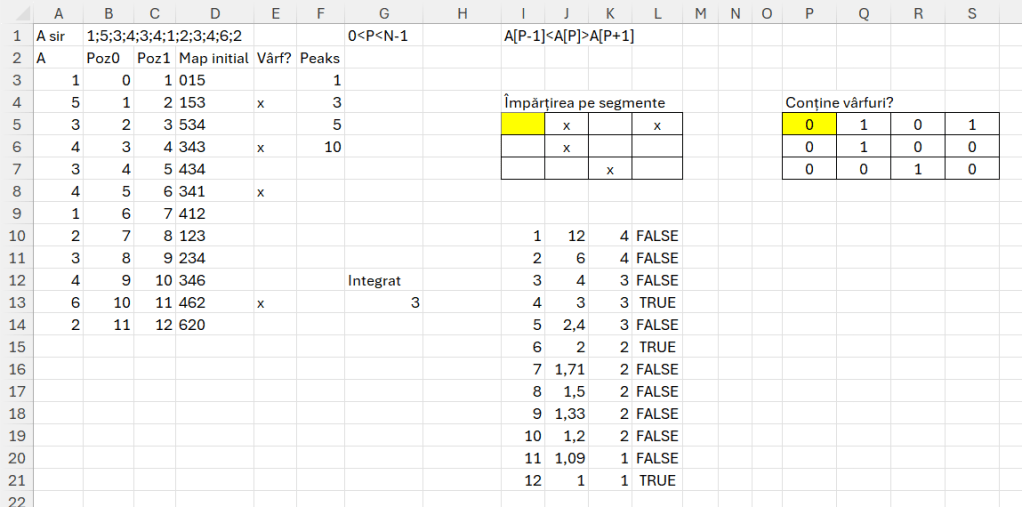
După cum se poate observa prima parte a problemei este asemnătoare cu Flags pentru că se obțin valorile vârfurilor. Apoi în I5 am folosit un WRAPROWS de vectorul cu vârfuri și am introdus manual valoarea coloanelor pe fiecare linie (2,3,4,5) pentru a obține cel puțin un x pe fiecare linie. În P5 am introdus funcția =IFERROR(FIND(„x”;I5#);0) pentru a calcula 1 sau 0 în funcție dacă conține x sau nu. Calculând suma pe linie putem vedea dacă numărul de segmente este optim. Numărăm apoi numărul de linii rezultat în funcție de dimensiunea vecotorului inițial și stabilim numărul de segmente în care se împarte optim vectorul, în cazul nostru 3. În zona I10 am unificat I5 și P5 pentru a putea calcula pe baza vectorului de vârfuri care este impărțirea optimă în segmente. observăm din tabel pe ultima coloană că putem avea mai multe valori adevărate pentru poziția 4, 6, 12, dar pe noi ne interesează numărul cel mai mic pentru că aceste valori reprezintă de fapt dimensiunea sub-segmentului iar coloana 3 numărul de linii rezultat care înseamnă total segmente. Conform cerinței problemei avem nevoie de cât mai multe segmente, dar pentru că pe coloana 2 nu obținem un număr egal (numărul de x pe fiecare linie) nu avem egalitate între coloana 2 și 3 pentru valoarile cu 4 segmente.

Bazându-mă pe experiența de lucru, am integrat toate funcțiile de pe parcurs în G13, funcția finală care determină optimul de subsegmente rezultat este:

=LET(gi; LET( a; TEXTSPLIT(B1;;";");
             _poz0; SEQUENCE(ROWS(a);;0);
             _poz1; SEQUENCE(ROWS(a);;1);
             gindex; MAP(_poz1;
                        LAMBDA(v; LET(_p_1;IF(v=1;0;INDEX(a;v-1));
                                      _p;INDEX(a;v);
                                      _p_2;IFERROR(INDEX(a;v+1);0);
                                      IF(AND(_p_1<_p;_p>_p_2);"x";""))));
            gindex);
    rrgi; ROWS(gi);
    freq; LAMBDA(v; LET(ver; WRAPROWS(gi;v);
                        findver; IFERROR(FIND("x";ver);0);
                        rfv; ROWS(findver);
                        tabrez; BYROW(findver;LAMBDA(r;SUM(r)));
                        rowstr;ROWS(FILTER(tabrez;tabrez>0;0));
                rowstr));
    runfreq; MAKEARRAY(rrgi;1;LAMBDA(r;c;freq(r)));
    tabi;HSTACK(SEQUENCE(rrgi);rrgi/SEQUENCE(rrgi);runfreq;rrgi/SEQUENCE(rrgi)=runfreq);
    rezfin; MAX(CHOOSECOLS(FILTER(tabi;(TAKE(tabi;;-1)));3));

rezfin
)

în care cheia este funcția recursivă freq care generează pentru fiecare valoare a lui r din runfreq un tabel de valori cu numărul de de x-uri pe care le avem pe fiecare segment.

gi este echivalentul vecotorului cu vârfuri din E3#.
rrgi este numărul de linii pe care le are vectorul de start, echivalent numerelor din șirul B1.
runfreq este echivalentul coloanei 3 din tabelul de testare prezentat anterior. El ne spune câte linii ar conține vârfuri (valoarea X) dacă am imparti vectorul în segmente de numărul celor specificate pe coloana 1 din tabelul din imagine.
tabi unifică prin HSTACK valorile asemnănător tabelului de testare și apoi inm rezfin facem filtrarea tabelului pe valoarea maximă de pe runfreq care îndeplineste criteriul de true.

Aplicații practice

Analiza pieței: Poate fi folosită pentru a analiza ciclurile economice, divizând datele financiare în perioade de creștere și declin, asigurându-se că fiecare perioadă conține un punct maxim.
Planificarea operațiunilor: În producție, poate ajuta la divizarea unui proces în etape, fiecare etapă având un punct de control sau un obiectiv intermediar atins.
Gestionarea resurselor: În logistica, problema poate ajuta la optimizarea rutelor, asigurându-se că fiecare segment al rutei include o oprire sau un punct important.

Cam atât pentru acest articol. Excelul poate destul de mult… important în schimb este să exersăm pentru a putea rezolva probleme cât mai complete în mod cât mai automatizat.

Sper să fie util cuiva!

22/08/2024

Modele de algoritmi în #Excel – Maximum slice problem (9)

În acest articol propun o metodă de rezolvare a algoritmilor clasici în formatul Excel modern, din categoria Maximul slice. Descrierea acestor probleme o găsiți la adresa: https://app.codility.com/programmers/lessons/9-maximum_slice_problem/

Puțină teorie

Pentru rezolvarea problemelor din acest articol am ales să folosesc cu precădere funcția MAKEARRAY() care poate avea o putere nebănuită de a transforma un vector liniar într-o matrice dacă reușești o proiecție corectă. Sintaxa funcției:

=MAKEARRAY(rows; columns; function) în care rows este numărul de linii care se vor genera cu începere de la R1 , columns la numărul de coloane din tabelul rezultat iar function este o funcție lambda() cu doi parametri: rows; columns.

După cum se observă în C2 este generată o matrice cu 9 linii și nouă coloane, pentru fiecare celulă realizându-se calculul r+c, însemnând valoarea rândului cu valoarea coloanei.

Celelalte funcții le-ați mai întâlnit. Mai multe detalii despre Filter puteți găsi în articolul de demult: Funcția Filter() din #Excel 365. Funcția Index() mi-a dat ceva de furcă la problema a treia… dar să ajungem acolo.

Să nu uităm că în algoritmică elementele unui vector încep de la 0, dar în Excel majoritatea operațiunilor de indexare/filtrare/cautare încep de la valoarea 1.

Problema MaxProfit

Face parte din categoria problemelor care analizează secvențe și se concentrează pe identificarea profitului maxim care poate fi obținut printr-o singură tranzacție de cumpărare și vânzare a acțiunilor.

Descrierea problemei: Ni se dă un vector A care conține prețurile acțiunilor în diferite zile. Trebuie să găsim profitul maxim care poate fi obținut cumpărând acțiunile într-o zi și vânzându-le într-o altă zi ulterioară. Dacă nu este posibil să obținem un profit (de exemplu, prețurile scad sau rămân constante), profitul ar trebui să fie considerat 0.

Propunerea de rezolvare:

În zona de Proiecție am realizat o implementarea manuală pentru a verifica suma maximă. La urma urmei multe probleme le rezolvăm manual până să ne mai chinuim să facem tot felul de funcții, nu? :) După ce am pus zilele și valoarile pe coloană și linie, la E3 am scris formula: =IF($C3<=E$1;””;$D3-E$2) , întotdeauna zilele trebuie să fie mai mici decât cele pentru care ne raportăm (axa timpului).

Apoi în C13 am proiectat o funcție integrată pentru a face din prima același tabel dar de data aceasta raportându-mă la vectori intermediari prin intermediul valorii lui r și c din makearray. Astfel funcția din C13 este:

=LET(arr; A2:A7; 
     seq; SEQUENCE(ROWS(arr)); 
     tarr; TRANSPOSE(arr); 
     tabi; MAKEARRAY(MAX(seq); MAX(seq); LAMBDA(r;c;
                   IF(r<=c;""; INDEX(arr;r)-INDEX(tarr;c)))); tabi)

în care arr stochează vectorul cu sumele de interpretat, seq generează numărul de zile, tarr transpozează numărul de zile pe coloane ca să le pot folosi ca artificiu în tabi care este de fapt un tabel care indexează valorile din arr pe baza liniei și coloanei curente.

Ulterior în D10 facem un max din acel tabel și avem rezultatul final. Ca să obținem și zilele în care avem acele valori în cazul nostru 1 și 5, atunci trebuie să apelăm șa tehnica de identificare a unei valori într-un tabel, descrisă în articolul: Modele de algoritmi in #Excel – Prefix Sums (5.1)

Problema MaxProfit este o problemă clasică de optimizare cu aplicabilitate în diferite contexte financiare în vederea rezolvării problemelor de maximizare a câștigurilor într-o serie de tranzacții.

Problema MaxSliceSum

MaxSliceSum este o problemă clasică în informatică, care face parte din categoria problemelor de optimizare pe secvențe, adică Maximum Subarray Problem.

Descrierea Problemei: Se dă un vector A de numere întregi (pozitive, negative sau zero). Trebuie identificată suma maximă a unui „slice” (subsecvență continuă) din acest vector. Un slice este definit de două indici P și Q din vectorul A, unde P ≤ Q, și include toate elementele de la A[P] până la A[Q].
Este posibil ca toate numerele să fie negative într-un vector, caz în care slice-ul cu suma maximă va fi cel mai mic număr negativ.

La o primă lectură a problemei am crezut ca este asemanator cu: Problema MinAvgTwoSlice, doar că de data aceasta nu mai luăm perechi de câte două elemente ci pot fi toate elementele… dintr-un șir sau doar o secvență P-Q.

Uneori problemele simple ne dau cele mai multe bătăi de cap, așa că a trebuit să mă documentez mai bine, și așa am aflat că de fapt această problemă mai este cunoscută și ca problema subșir de sumă maximă sau Algoritmul lui Kadane, unul foarte cunoscut în lumea programatorilor. Mi-au plăcut foarte mult explicațiile din filmulețul: Algoritmul lui Kadane – Determinarea unui subsir de suma maxima in C++

Să revenim la Excel. După multe încercări și teste am ajuns din nou la funcția Makearray care are o putere nebănuită în bi-dimensional prin parametrii săi r și c din LAMBDA asociat.

În final implementarea algoritmului este ceva spectaculos de simplu și puternic:

În zona de proiecție matrice am creat un array în care pentru fiecare r<=c am făcut suma subvectorilor de la linia curentă până la coloana curentă.

Funcția din E3 este:

=MAKEARRAY(8;8; LAMBDA(r;c; IF(r<=c; SUM(INDEX($A$2:$A$9;r):INDEX($A$2:$A$9;c));””)))

în care pentru fiecare celulă din tabelul 8 pe 8 calculăm suma valorilor indexului dinamic de la r la c. Comparați cu complexitatea din filmulețul cu implementarea în C++ și poate dați o șansă Excelului. :) Dincolo de glumă pe mine m-a încântat mult soluția, dar vom vedea la următoarea problemă că lucrurile nu sunt chiar atât de roz în Excel….

Funcția integrată care extrage și slice-ul cu sumă maximă este:

=LET(arr; A2:A9; 
     seq; SEQUENCE(ROWS(arr)); 
     rr; ROWS(arr);
     fSlice; LAMBDA(x; LET(aria;x; 
                           ca; MIN(COLUMN(aria))-1; 
                           ra; MIN(ROW(aria))-1;
                           tc; TOCOL(aria;1);
                           unde; MATCH(MAX(aria);tc;0);
                           col; LET(cs; COLUMNS(aria);
                                    c; MOD(unde;cs);
                                     IF(c=0; cs; c));
                           row; ROUNDUP(unde/COLUMNS(aria);0); 
                                "("&row-1&","&col-1&")"));
sarr; MAKEARRAY(rr; rr; LAMBDA(r;c; 
                               IF(r<=c; SUM(INDEX(arr;r):INDEX(arr;c));""))); 
                               "Smax: "&MAX(sarr)&" - Slice: "&fSlice(sarr))

Toată construcția pare mai complicată pentru că am integrat în fSlice tehnica de identificare a locației unei coloane, în vederea afișării slice-ului maxim. Dar toată cheia soluției este în variabila sarr în care am acel MAKEARRAY descris anterior, doar că de data aceasta dinamic pe baza variabilelor definite la început.

Din păcate pentru multe numere în A, Excelul începe să gâfâie. La 1024 de numere algormitmul merge foarte bine dar la 4096 a început deja să dea semne de blocare. Pentru testare am utilizat funcția de generare array aleatoriu: =RANDARRAY(128;1;-50; 200;TRUE) în care se generează 128 de numere întrgi (TRUE) de la minim -50 până la maximum 200. Limita de numere din A este limita numărului de coloane din Excel (16384) pentru a putea opera matricea de calcule.

MaxSliceSum este util în analizarea datelor financiare (de exemplu, determinarea perioadei în care profitul a fost maxim) sau în analizarea performanței sistemelor (de exemplu, identificarea perioadelor de maximă încărcare sau activitate). Această problemă este importantă pentru înțelegerea optimizărilor pe secvențe și este un exemplu clasic de aplicare a algoritmilor de programare dinamică.

Problema MaxDoubleSliceSum

Problema MaxDoubleSliceSum este o extindere a problemei MaxSliceSum, fiind parte din categoria problemelor de optimizare pe secvențe. Scopul este să găsești suma maximă posibilă a unei subsecvențe formate din trei părți neconsecutive dintr-un vector.

Descrierea Problemei:
Se dă un vector A de numere întregi de lungime N (unde N ≥ 3). Trebuie calculată suma maximă posibilă a unui double slice (subsecvență non-consecutivă) definită de trei indici X, Y, și Z (unde 0 ≤ X < Y < Z < N).
Double slice-ul este definit astfel:
– X este începutul primei secțiuni care este exclusă.
– Y este începutul secțiunii incluse în sumă.
– Z este sfârșitul secțiunii incluse, care este exclusă din sumă.
Suma double slice-ului este calculată ca suma tuturor elementelor din A[X+1] până în A[Y-1] și din A[Y+1] până în A[Z-1].
Rezolvarea algoritmului a fost o mare provocare pentru că indexarea nu funcționează absolut deloc într-un context prea dinamic, de aceea a trebuit să găsesc o altă metodă de rezolvare.

Propunere rezolvare problema MaxDoubleSliceSum

În rezolvarea problemei am pornit de la metoda propusă în Problema MaxProductOfThree doar că de data aceasta nu mă mai refer unitar la poziția lui X, Y sau Z ci trebuie să caut în șirul A valorile echivalente din matrice și să le însumez. În rezolvarea pas cu pas am generat întâi matricea XYZ cu toate combinațiile posibile în care X<Y<Z. Apoi pe bază de indexare în I4 am calculat suma elementelor. Funcția utilizată linie cu line:

=LET(arr;$A$2:$A$9; 
     rr; E4:G4; 
     x; --TAKE(rr;;1); 
     y; --CHOOSECOLS(rr;2); 
     z; --CHOOSECOLS(rr;3); 
     SUM(IF(x+1=y;0;
           INDEX(arr;x+1):INDEX(arr;y-1));
         IF(y+1=z;0;
            INDEX(arr;y+1):INDEX(arr;z-1))))

variabilele x, y și z sunt preluate pentru fiecare linie apoi fac suma prin indexarea de la X+1 la Y-1 și de la Y+1 la Z-1. Merge destul de bine dar nu am reușit să le integrez în aceeași funcție pentru că modelul este prea elaborat pentru a putea să funcțineze funcția INDEX():INDEX().

Ca să pot identifica și studia care sunt valorile care compun rezultatul am creat coloana intermediară K în care am unificat prin aceeași tehnică de indexare dinamică a vectorului A, pe baza valorilor din matrice.

Unificarea într-o singură formulă a fost un coșmar, insistând pe INDEX():INDEX() și câteva zeci de variante de funcții recursive. Până la urmă am realizat că FILTER() cu criterii multiple este mai fezabil pentru că returrnează blocuri de celule însumabile.

Funcția finală din N5 este:

=LET(arr; A2:A9; 
     seq; SEQUENCE(ROWS(arr));
     matrix; LET(vector; arr;
                nr; ROWS(vector);
                matrix; MAKEARRAY(nr^3; 3; 
                         LAMBDA(i;j; 
                          IF(j = 1; 
                            INT((i-1)/nr^2)+1; 
                            IF(j = 2; MOD(INT((i-1)/nr); nr)+1;
                                     MOD(i-1; nr)+1))));
   fReq; LAMBDA(x; AND(INDEX(x;1)<INDEX(x;2);INDEX(x;2)<INDEX(x;3)));
   verif; BYROW(matrix; LAMBDA(r; fReq(r )));
   tabi; HSTACK(matrix; verif);
   unics; FILTER(tabi; (TAKE(tabi;;-1)=TRUE)*(CHOOSECOLS(tabi;3)<nr));
   unicsm; CHOOSECOLS(unics;1;2;3);
   unicsm);

tabf; HSTACK(arr;seq);
slice; BYROW(matrix; LAMBDA(r; TEXTJOIN(";";;r-1)));
fcautxy; LAMBDA(a;b; 
                SUM(TAKE(IFERROR(FILTER(tabf; 
                      (TAKE(tabf;;-1)>=a+1)*(TAKE(tabf;;-1)<=b-1));0);;1)));
fcautxyz; LAMBDA(x;y;z; fcautxy(x;y)+fcautxy(y;z));

summax; BYROW(matrix; 
        LAMBDA(r; LET(x; TAKE(r;;1); 
                      y; TAKE(TAKE(r;;2);;-1); 
                      z; TAKE(r;;-1); 
                    fcautxyz(x;y;z))));
maxsum; MAX(summax);

tabfin; HSTACK(slice; summax);
FILTER(tabfin; TAKE(tabfin;;-1)=maxsum))

în care:

variabila matrix este definită în articolul Problema MaxProductOfThree și este utilizat doar pentru a putea genera matricea de căutare cu X<Y<Z toate combinațiile posibile.
tabf este de fapt tabelul cu coloana A și secvența de numere în format de start de la 1 pentru a putea să realizez indexarea pe această coloana.
slice este utilizată pentru a putea genera perechile de x;y;z în formatul array cu start de la 0 rezultatul fiind afișat ulterior în tabfin.
fcautxy este o funcție recursivă pe care o folosesc mai jos în fcautxyz pentru ca putea extrage cu filter valorile din A, stocate pe prima coloana a lui tabf pe care o preiau cu TAKE(). Simbolul * este folosit pentru condiții cumulative în filter(). Sintaxa pe cumulative este Filter(valori; (Cond1)*(Cond2) ). Filter() a fost soluția salvatoare.
fcautxyz este funcția recursivă care face suma prin filtrare, definită în fcautxy dar cu aplicare pe Xy și yz. Aici este artificiul suprem prin care am putut folosi o recursivă în atltă recursivă pentru a adresa din două poziții diferite vectorul A.
summax este un vector de valori intermediare care preia linie cu linie (BYROW) din matrix valorile lui X, Y, Z după care invocă recursiva fcautxyz pentru a calcula suma.
maxsum calculează valoarea maximă obținută pe summax
tabfin este tabelul final în care unesc valoarea maximă cu slice după care în rezultatul afișat introduc un nou FILTER de data aceasta pe tabel, în care valoarea obținută să fie egală cu maximum obținut în maxsum.

Huh… a luat ceva timp… dar merită efortul… cu toate că la testare am avut neplăcuta surpriză să constat că numărul maxim de numere din A este de 101… de ce? pentru că rădăcina cubică a numărului maxim de linii din excel (1.048.576) este aproape 101,5…

Aici ajungem la prima limitare a Excelului în rezolvarea acestui tip de probleme. Voi reveni cu o imbunătățire a matricei de triplete care funcționează până la 185 de linii. Veți vedea de ce.

Ca aplicații practice pentru această problemă mă gândesc acum la finanțe, identificarea intervalelor de creștere și scădere a valorii acțiunilor, pentru a găsi cele mai profitabile perioade de vânzare și cumpărare.
sau analiza datelor pentru găsirea secvențelor de date cu cea mai mare variabilitate pozitivă, utile în detectarea anomaliilor sau în analiza trendurilor.

Cam atât pentru astăzi.

Sper să fie util cuiva!

14/08/2024

Modele de algoritmi in #Excel – Leader (8)

Acest articol este o continuare a seriei de articole cu propunere de rezolvare a algoritmilor clasici în Microsoft Excel ediția 365. Probelemele de astăzi fac parte din algoritmii Leader descriși la adresa: https://app.codility.com/programmers/lessons/8-leader/

Algoritmul Leader se referă la identificarea unui element dintr-o secvență de valori care apare mai mult de jumătate din numărul total al elementelor din acea secvență. Acest element este denumit „leader” sau „dominator”. Problema se poate formula astfel: având un vector de dimensiune N, să se găsească elementul care apare de cel puțin N/2 + 1 ori, dacă există unul. În mod programatic se recomandă rezolvarea acestor tipuri de probleme cu algoritmul Boyer-Moore majority vote.

Doar că Excelul este puțin diferit și este mai greu de adaptat la rezolvările clasice care implică secvențe FOR. Alternative există și unele din ele sunt foarte interesante. Dar să începem cu:

Un pic de teorie

În mod clasic dacă am avea un șir de numere sau valori ar trebui să identificăm unicele, apoi să facem un countif pe blocul inițial.

De exemplu în E3: folosim funcția UNIQUE() pentru a calcula elementele unice din vectorul A2:A7, după care utilizăm un COUNTIF() dinamic pe vector după rezultatul din E3#. În felul acesta determinăm numărul de apariții a fiecărui element. Există și o variantă puțin diferită, de a folosi funcția FREQUENCY() în forma: =FREQUENCY(A2:A7; UNIQUE(A2:A7)) dar ea determină doar numărul de apariții a fiecărui element, în cazul nostru 3/3.

În Excel în schimb există o altă funcție MODE cu două variante: SNGL sau MULT. MODE.SNGL() extrage dintr-un șir de valori cea prima cea mai frecventă valoare. În exemplu nostru (B3) avem două valori care au același număr de apariții, ceea ce înseamnă că va afișa doar prima valoare întâlnită în vectorul de căutare. MODE.MULT() extrage cele mai frecvente numere, în cazul în care avem egalitate la numărul de apariții le va afișa pe ambele. În cazul în care nu avem nici un leader, funcția MODE va afișa eroarea #N/A.

O abordare interesantă este în schimb la text, pentru că MODE.MULT() funcționează doar la valori numerice. În modelul propus în imaginea anterioară, ca să putem determina leaderul folosim un MODE dar pentru un MATCH care extrage pentru fiecare valoare întâlnită poziția inițială a sa. După care pe același șir extragem valoare pentru cea mai mare valoare. MODE() în formatul clasic încă este funcțional și compatibil în Excel 365.

Problema Dominator

În problema Dominator ni se cere să determinăm care este numărul dintr-un vector care apare de mai mult de jumătate din lungimea vectorului. De asemenea, se poate solicita extragerea pozițiilor din vector în cazul în care avem un număr Dominator.

Propunerea de rezvare pas cu pas:

Ca să determin Leader-ul este simplu să folosim un MODE.MULT() în E3, dar ca să determinăm dacă este dominiator avem nevoie de numărul de elemente din vector (B2), valoarea de dominare care este numărul de elemente împărțit la 2 (C2), numărul de apariții (F2), verificarea că Leaderul este dominator (G2), iar dacă dorim să extragem pozițiile în vector va trebui să folosim o secvență cu start de la 0 (D2) pe care să o filtrăm după pentru cazurile în care A este egal cu Leader care devine dominator.

Unificat într-o singură funcție cu LET() aceasta ar fi:

=LET(arr; A2:A9;
     nrEl; ROWS(arr);
     dominatorv; nrEl/2;
     seq; SEQUENCE(nrEl;;0);
     dominator; MODE.MULT(arr);
     verifi; ROWS(dominator)=1;
     aparitii; COUNTIF(arr; dominator);
     verifii; aparitii>dominatorv;
     IF(AND(verifi; verifii);
          TEXTJOIN("; "; ; FILTER(seq; arr=dominator));
          "Nu există dominator"))

În funcție am două verificări: verifi și verifii. În verifi verific dacă am un singur rezultat sau mai multe. În cazul în care sunt returnate mai multe valori prin MODE.MULT atunci nu avem un dominator ci mai mulți Leaderi. În rest logica funcției este descrisă în secțiunea de rezolvare pas cu pas.

Problema EquiLeader

Aceasta este o versiune mai complexă a problemei Dominator pentru că presupune compararea dinamică a leaderilor pe două secțiuni ale aceluiași vector. În această problemă, trebuie să determinăm numărul de poziții dintr-un array unde liderii celor două sub-secvențe (stânga/sus și dreapta/jos) sunt identici. Concret: Având un array A de dimensiune N, o poziție S este un echileader dacă liderul sub-secvenței A[0…S] este același cu liderul sub-secvenței A[S+1…N-1]. Trebuie să găsim numărul total de astfel de poziții în array.

După citirea enunțului am realizat că logica de rezolvare este identică cu problema TapeEquilibrium din articolul Modele de algoritmi in #Excel – Time complexity (3) .

Propunere rezolvare în Excel:

În care pe coloana C determinăm dacă în poziția curentă comparată cu celelaltă secțiune avem egalitate de Dominatori, iar pe coloana D afișăm combinațiile de pe secvența de pe B. Funcția de pe C și D este aceeași cu specificarea că rezultatul final este afișat diferit.

=LET(arr;A2:A7;poz;SEQUENCE(ROWS(arr);;1);
freq; LAMBDA(a; LET(x; a; cate; ROWS(x); unice; UNIQUE(x); dominatorv; cate/2; nrfiecare; COUNTIF(x; unice); tabi; SORT(HSTACK(unice; nrfiecare);2;-1); dominatorval; TAKE(tabi;1;-1); veri; dominatorval>dominatorv; dominator; IF(veri; TAKE(tabi;1;1); 0); dominator));

pp;MAP(poz;LAMBDA(v; LET(ari; INDEX(arr;1):INDEX(arr;v); freq(ari))));
ppa; LET(pozi; B2#; ppa; MAP(pozi;LAMBDA(v; TEXTJOIN(";";;INDEX(pozi;1):INDEX(pozi;v+1)))); ppa);

dp;MAP(poz;LAMBDA(v; LET(arii; (INDEX(arr;v+1):INDEX(arr;ROWS(arr))); freq(arii))));
dpa;LET(pozi; B2#; ppa; MAP(pozi;LAMBDA(v; TEXTJOIN(";";;INDEX(pozi;v+2):INDEX(pozi;ROWS(arr))))); ppa);

domins;IFERROR(pp=dp; "");
nrequi; SUM(IFERROR(--domins; 0));

care; IFERROR(IF(domins; ppa&" - "&dpa;"");"");
domins
)

Cheia în rezolvarea problemei, este funcția freq care este utilizată recursiv în MAP-ul care calculeaza valoarea pp și dp. freq este de fapt funcția de determinare a dominatorului din problema Dominator, dar care este generalizată pentru a prelua parametrul de intrare a, care se transformă în x în LET() și calculează dominatorul pe subvectorul determinat în pp și dp de index-ul dinamic.

ppa și dpa se folosesc pentru a extrage valoarea din secvență pentru a afișa pozițiile din vector și secțiunile unde întâlnim dominatori egali.

Rezultatul 2 al funcției este numărul de segmente de pe vector care înreplinesc condiția de egalitate între dominatori.

Ca aplicabilitate practică putem să ne gândim la analize de piață pentru a identifica dacă pe diferite segmente sau intervale de timp există un brand dominant.

Cam atât pentru astăzi!

Sper să vă fie util!

31/07/2024