Nu am idee cum s-ar traduce cel mai bine în limba română această metodă. Unii spun că ar fi metoda omidei alți autori metoda ferestrei glisante bidirecționale. Scopul meu este să rezolv în Excel problemele din această categorie, rezolvări care mi s-au părut relativ simple în Excel.
Mă apropii de finalul problemelor de pe Codility, iar astăzi vă propun câteva metode de rezolvare din cadrul probemelor Caterpillar method explicate la această adresa: https://app.codility.com/programmers/lessons/15-caterpillar_method/
Denumirea vine de la modul în care algoritmul își extinde și retrage fereastra de procesare, similar cu modul în care o omida se mișcă – înaintează secvențial, dar își ajustează poziția astfel încât să acopere eficient o zonă, fără suprapuneri inutile.
În Excel operațiunile acestea le putem face prin indexarea unui vector în funcție de diferite poziții curente de căutare, adresabile prin variabilele R și C ale lui MAKEARRAY() sau cele 3 valori ale matricelor de triplete TripleG (denumire pe care o dau eu acestei tehnici descrise în mai multe ocazii).
Dar înainte de a începe să prezentăm…
Foarte puțină teorie
Pentru a secvenția un vector sau un tabel în Excel avem la dispoziție mai multe funcții, modul în care le utilizează fiecare dintre noi depinzând de experiență, inspirația de moment sau cunoașterea lor.
Principalele funcții pe care le adresez în această secțiune sunt: TAKE(), CHOOSECOOLS(), COOSEROWS(), DROP(), INDEX().

INDEX() în combinație cu MATCH() a fost mult timp considerat o alternativă la VLOOKUP(). Doar că această funcție poate face mult mai mult chiar dinainte de funcțiile dinamice, când artificiul suprem erau funcțiile CSE (Ctrl+Shift+Enter). Combinat cu SEQUENCE() în versiunile moderne de Excel nu mai este nevoie să introducem funcția cu CSE ci funcționează automat. Plus dinamica lui Sequence ne poate duce la soluții extraordinar de spectaculoase. Vezi exemplul din A14 unde aducem ultimele 3 numere din tabel de pe ultima coloană în ordine inversă.
Avantajul lui DROP și TAKE este că pot adresa atât linii cât și coloane prin parametrii 2 și 3. Coloanele și liniile pot fi adresate cu numere pozitive în ordinea coloanelor (1 prima coloana, 2 primele două coloane) cât și negative (-1 ultima linie/coloana, -2 ultimele două linii sau coloane). Choosecols sau Chooserows sunt oarecum mai precise pentru că adresează exact coloana sau linia specificată, dar pot fi și ele combinate cu SEQUENCE() pentru a adresa mai multe linii sau coloane. De exemplu în K6 putem face o optimizare cu sequence în forma: =CHOOSEROWS(COOSECOLS(vNumere;1); SEQUENCE(5;;2))
Personal consider că în cele mai multe cazuri INDEX() este de departe funcția câștigătoare, dar nu sunt de neglijat nici celelalte cazuri de utilizare.
Sortarea valorilor pe linie?!
Într-o zi una din firmele cu care lucrez pe partea de training privat de Excel mi-a trimis o agendă personalizată pentru un curs de Excel Avansat în care unul din puncte era sortarea valorilor pe linii. Eu când nu știu ceva, nu predau sau nu accept deloc clientul. Având în vedere că era totuși un client vechi și important am cerut clarificări… dar nu înainte de a mă uita pe internet dacă există așa ceva…
Ceea ce mi s-a confirmat și am găsit pe Internet mi s-a părut ceva simplist așa că am mers înainte. Dar cazul nu este deloc așa cum ar trebui.
Pentru versiunea manuală de sortare dacă vrei să faci sortarea pe linie:
Dacă vrei să sortezi valorile existente direct în tabel trebuie să parcurgi următorii pași:
- Selectează rândul cu datele pe care vrei să le sortezi.
- Mergi la „Home” sau „Data” → „Sort & Filter” → „Custom Sort”.
- În fereastra de sortare, apasă pe „Options” și selectează „Sort left to right”.
- Alege criteriul de sortare (ordine crescătoare sau descrescătoare) și apasă OK.
Având în vedere că în Excelul modern, operațiunile manuale sunt înlocuit cu funcții, operațiunea se poate realiza și prin funcția SORT() cu valoarea FALSE pentru parametrul 4.
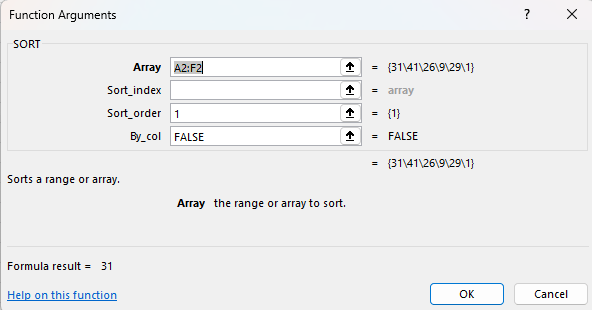
Și totuși dacă am dori să sortăm toate valoarile crescător pe fiecare linie în parte?
Lucrurile nu mai sunt la fel de simple pentru că funcția sort nu mai funcționează așa cum ne-am aștepta. În Excel, SORT() este dedicat implicit valorilor de pe o coloană, iar ca să ducem o linie în coloană folosim TRANSPOSE().
Exemplificare valori random:

Pentru această operațiune introduc în acest articol funcția _fSortRows() care are următorul corp:
=LET(arr; A2:F25;
join; BYROW(arr; LAMBDA(r; TEXTJOIN(";";;r)));
rez; MAP(join; LAMBDA(x; TEXTJOIN(";";;SORT(TRANSPOSE(--TEXTSPLIT(x; ";"))))));
result; TEXTSPLIT(TEXTJOIN("|";TRUE;rez);";";"|");
result
)în care:
- arr – este blocul de numere generat aleator cu RADARRAY();
- join – unește toate valorile de pe linie pentru a le putea parcurge linie cu linie cu MAP() din rez;
- result – este rezultatul cu artificiul de splitare a blocurilor de valori pe linii și coloane.
Această parte am sintetizat-o și într-un scurt clip video.
Acestea fiind spuse, să trecem la rezolvarea problemelor:
Problema AbsDistinct
Problema AbsDistinct presupune determinarea numărului de valori distincte dintr-un array, luând în considerare doar valoarea absolută a fiecărui element.
Exemplu
Dacă avem următorul array sortat: -5,-3,-1,0,3,6
Valorile absolute sunt: 0,1,3,3,5,6
Valorile distincte sunt: 0, 1, 3, 5, 6 (5 valori distincte).
Rezolvarea este foarte simplă în Excel:

în C2 am utilizat formula: =SORT(UNIQUE(ABS(A2:A7)))
în care ABS calculează absolutul fiecărui număr din vectorul A, UNIQUE() determină toate valorile unice, iar SORT() le sortează ascendent.
Această metodă poate fi utilizată în cazul tranzacțiilor bursiere pentru a identifica variațiile unice absolute ale unei acțiuni într-o perioadă de timp.
Problema CountDistinctSlices
În cardrul acestei probleme avem un șir de numere (A) și vrem să determinăm câte sub-secvențe distincte (numite și slice-uri) pot fi formate, astfel încât toate elementele din fiecare sub-secvență să fie distincte.
Scopul problemei este să aflăm câte sub-secvențe (slice-uri) distincte există, astfel încât niciun număr dintr-un slice să nu se repete.
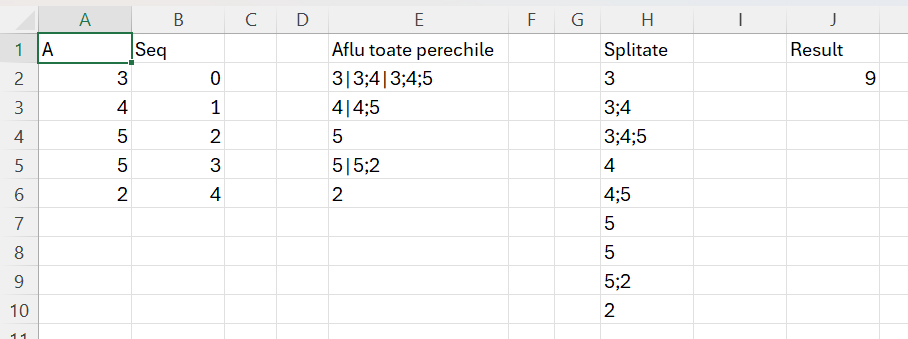
Rezolvarea problemei nu a fost chiar atât de simplă cum pare la final din cauză că nu am identificat de la început calea cea mai simplă de rezolvare, eu abordând matricial problema cu Makearray(). Doar că matricile nu rezolvă problema sau cel puțin nu am identificat calea corectă.
Rezultatul sugerat de cei de la Codility era dat de următoarele combinații unice: (0, 0), (0, 1), (0, 2), (1, 1), (1, 2), (2, 2), (3, 3), (3, 4) and (4, 4) eu personal neînțelegând la început că slice (0,2) înseamnă valorile 3,4,5.
Ca să pot rezolva problema am introdus în E2 o formulă destul de abstractă pe care încercă să o explic:
=MAP(B2#;
LAMBDA(poz;
TEXTJOIN("|";;
SCAN(0; DROP($A$2:$A$6;poz);
LAMBDA(a;v;
IF(a=0; v;
IF(IFERROR(TAKE(--TEXTSPLIT(a;";");;-1);v)=v;
"";
IF(a="";"";TEXTJOIN(";";TRUE;a;v))
)
)
)
)
)
)
)Ca să pot scana blocul de la poziția 0, apoi de la poziția 1 și așa mai departe, a trebuit să definesc secvența din B2 pe care o parcurg cu MAP(). Apoi pentru fiecare poziție, returnez o combinație de valori de pe blocul A2:A6 pe care-l parcurg cu SCAN(). Partea frumoasă a acestei construcții este dată de faptul că în acumulatorul a introduc întotdeauna valorile în ordinea lor, ceea ce-mi permite să le iau cu acel TAKE() pentru a-l putea compara cu valoarea curentă V ca să identific dacă valorile sunt egale. Scan-ul funcționează la început pentru valoarea 0 a vectorului din B2#. Apoi map-ul duce Scanul mai jos pentru restul de slices.
În H2 folosesc artificiul de splitare: =TEXTSPLIT(TEXTJOIN(„|”;;E2#);;”|”)
Integrate toate operațiunile într-o singură formulă ar arăta:
=LET(_a; A2:A6; seqa; SEQUENCE(ROWS(_a);;0);
perechi; MAP(seqa; LAMBDA(poz; TEXTJOIN("|";;
SCAN(0; DROP(_a;poz); LAMBDA(a;v; IF(a=0; v;
IF(IFERROR(TAKE(--TEXTSPLIT(a;";");;-1);v)=v;"";
IF(a="";"";TEXTJOIN(";";TRUE;a;v)))))))));
rezi; TEXTSPLIT(TEXTJOIN("|";;perechi);;"|");
result; ROWS(rezi);
result
)în care în variabila prerechi calculez acel MAP cu SCAN integrat.
O variantă oarecum diferită a acestei soluții este să oprim SCAN-ul în momentul în care o valoare din A se repetă anterior. Exemplificare:

În acest context când în prima rundă de scanare apare varianta 3 care este deja mai sus, se oprește scan și trece la secvența următoare. Pentru aceasta folosesc o funcție ușor diferită dar cu aceeași logică.
=LET(_a; A27#; seqa; SEQUENCE(ROWS(_a);;0);
perechi; MAP(seqa; LAMBDA(poz; TEXTJOIN("|";;
SCAN(0;DROP(_a;poz);LAMBDA(a;v; IF(a=0;v;
IF(IFERROR(SUM((--(--TEXTSPLIT(a;";")=v)))>0;0);"";
IF(a="";""; TEXTJOIN(";";;a;v)))))))));
rezi; TEXTSPLIT(TEXTJOIN("|";;perechi);;"|");
result; ROWS(rezi);
UNIQUE(rezi)
)În prima variantă folosesc doar ultima valoare din acumulatorul a iar în varianta 2 compar toate valorile din acumulator cu valoarea curentă. De reținut aici că nu putem utiliza un COUNTIF() într-un SCAN așa că a trebuit să introduc artificiul de a compara oricare valoare din A cu V și transformarea în valori 0,1.
Problema CountTriangles
Problema CountTriangles se referă la identificarea tripletelor dintr-un șir de numere care pot forma triunghiuri valide conform inegalității triunghiului.
Inegalitatea triunghiului afirmă că, pentru trei laturi a,b,c ale unui triunghi, trebuie să se respecte condiția:
a+b>c , b+c>a, c+a>b
Într-un șir sortat, regula devine mai simplă: dacă avem trei elemente A[i],A[j],A[k] unde i<j<k , triunghiul este valid doar dacă: A[i]+A[j]>A[k].
Ca să putem compara oricare 3 elemente dintr-un vector avem nevoie de matricea de triplete introdusă în articolul Modele de algoritmi in #Excel – Sorting (6). De asemenea, problema triunghiurilor a mai fost tratată în articolul menționat la Problema Triangle. De asemenea, a fost descrisă puțin mai pe larg în articolul Programarea funcțională în Excel Modern din pinmagazine.ro una din ultimele reviste de IT, pe care le cunosc eu, disponibilă și offline.
Scopul matricei de triplete este de a genera toate combinațiile unice de câte 3 valori corespunzătoare indexului valorilor pozițiilor unui vector A cu începere de la 1. În articolul din PIN Magazine scriam că această matrice este echivalentului unui triplu FOR din programare. Reamintesc funcția de generare a matricei de indecsi unici.
=LET(sir;R1;split; TEXTSPLIT(sir;;";"); nrElemente; ROWS(split);
combinatii; COMBIN(nrElemente; 3);
TripleG; SCAN("1;2;2"; SEQUENCE(combinatii);
LAMBDA(a;v;
LET(arr; --TEXTSPLIT(a;";");
x; TAKE(arr;;1); y; TAKE(TAKE(arr;;2);;-1); z; TAKE(arr;;-1);
newx; IF(AND(y=nrElemente-1; z=nrElemente);
IF(x<nrElemente-2; x+1; x); x);
newy; IF(newx=x; IF(z=nrElemente;
IF(y<nrElemente-1; y+1; y);y); newx+1);
newz; IF(newx=x; IF(z<nrElemente;z+1;y+2); newy+1);
newx&";"&newy&";"&newz)));
tabf; --TEXTSPLIT(TEXTJOIN("|";;TripleG);";";"|");
tabf)Această funcție este optimizată în raport cu numărul de elemente din șirul din R1 în cazul acesta pentru că suportă până la 185 de elemente în șir față de 101 în varianta din articolul 6.
Proiecție problemă în Excel

Formula din K3 este bazată pe o variantă a articolului 6 și este:
=LET(vector; A2:A7;
nr; ROWS(vector);
matrix; MAKEARRAY(nr^3; 3; LAMBDA(i;j; IF(j = 1; INT((i-1)/nr^2)+1; IF(j = 2; MOD(INT((i-1)/nr); nr)+1; MOD(i-1; nr)+1))));
fReq; LAMBDA(x; AND(INDEX(x;1)<>INDEX(x;2);INDEX(x;2)<>INDEX(x;3);INDEX(x;1)<>INDEX(x;3)));
verif; BYROW(matrix; LAMBDA(r; fReq(r )));
tabi; HSTACK(matrix; verif);
unics; FILTER(tabi; TAKE(tabi;;-1)=TRUE);
unicsm; CHOOSECOLS(unics;1;2;3);
fReqv; LAMBDA(x; CONCAT(INDEX(vector;INDEX(x;1));";";INDEX(vector;INDEX(x;2));";";INDEX(vector;INDEX(x;3))));
vals; BYROW(unicsm; LAMBDA(r; fReqv(r )));
sVals; UNIQUE(MAP(vals; LAMBDA(v; TEXTJOIN(";"; ; SORT(--TEXTSPLIT(v;;";"))))));
Split; --TEXTSPLIT(TEXTJOIN("|";1;sVals);";";"|");
fverif; LAMBDA(x;AND(INDEX(x;1)+INDEX(x;2)>INDEX(x;3);
INDEX(x;1)+INDEX(x;3)>INDEX(x;2);
INDEX(x;2)+INDEX(x;3)>INDEX(x;1)));
verift; BYROW(Split; LAMBDA(r; fverif( r)));
tabf; HSTACK(Split; verift );
triplef; TAKE(FILTER(tabf; TAKE(tabf;;-1)=TRUE;"0");;3);
triplef)În care în prima parte se generează matricea de căutare, după care prin funcția recursivă fReqv se indexează vectorul de valori A cu scopul de a determina inegalitățile de tipul a+b>c solicitate de problemă. În felul acesta determinăm că anumite combinații de numere pot reprezenta triunghiuri din punct de vedere geometric.
Problema MinAbsSumOfTwo
Având în vedere că este o problemă cu două valori dintr-un vector care trebuie comparate, soluția optimă în Excel este utilizarea unui MAKEARRAY().
Problema constă într-un vector de numere a cător sumă în format aboslut trebuie să fie cea mai mică. Formal, dacă avem un array A de dimensiune N, trebuie să determinăm: min(|A[i]+A[j]|) unde 0≤i≤j<N.
Proiecția problemei în Excel:
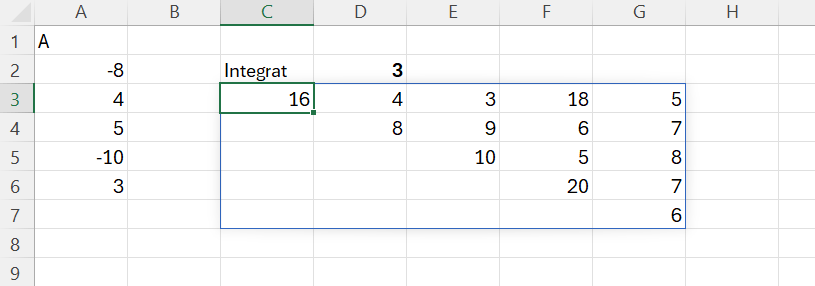
în care formula din C3 este:
=LET(arr; A2:A6; rr; ROWS(arr);
MAKEARRAY(rr;rr;LAMBDA(r;c;
IF(r>c;"";ABS(INDEX(arr;r)+INDEX(arr;c))))))în care matricea generată cu MAKEARRAY indexează vectorul arr pentru fiecare combinație de linie și coloană.
O variație a acestei probleme care nu există pe Codility este să determin mimimul sau maximul absolut a trei valori din vector. Această problemî în Excel ar arăta:

în care am utilizat din nou matricea de triplete, dar de data aceasta cu scopul de a păstra toate valorile posibile în matrice nu doar valorile unice.
Formula din D2 devine astfel:
=LET(arr;A2:A6;
seq; SEQUENCE(ROWS( arr));
matrix; LET(vector; arr;
nr; ROWS(vector);
matrix; MAKEARRAY(nr^3; 3;
LAMBDA(i;j;
IF(j = 1;
INT((i-1)/nr^2)+1;
IF(j = 2; MOD(INT((i-1)/nr); nr)+1;
MOD(i-1; nr)+1))));
fReq; LAMBDA(x; AND(INDEX(x;1)<INDEX(x;2);INDEX(x;2)<INDEX(x;3)));
verif; BYROW(matrix; LAMBDA(r; fReq(r )));
tabi; HSTACK(matrix; verif);
unics; FILTER(tabi; (TAKE(tabi;;-1)=TRUE)*(CHOOSECOLS(tabi;3)<=nr));
unicsm; CHOOSECOLS(unics;1;2;3);
TAKE(tabi;;3));
summax; BYROW(matrix;
LAMBDA(r; LET(x; TAKE(r;;1);
y; TAKE(TAKE(r;;2);;-1);
z; TAKE(r;;-1);
ABS(INDEX(arr;x)+INDEX(arr;y)+INDEX(arr;z)))));
HSTACK(matrix; summax))Cam atât pentru astăzi… să aveți o săptămână productivă și
Sper să fie util cuiva!
