După o perioadă de pauză în care au fost multe de făcut, dar și datorită unor probleme de optimizare a codurilor și formulelor, reiau seria de articole din categoria algoritmilor clasici cu propuneri de implementare / rezolvare în Excel.
În articolul de astăzi voi trata colecția de probleme Sorting de pe Codility: https://app.codility.com/programmers/lessons/6-sorting/
Un pic de teorie
Algoritmii de sortare sunt proceduri care rearanjează elementele unei liste (sau altor structuri de date) într-o anumită ordine, de obicei crescătoare sau descrescătoare. Acești algoritmi sunt esențiali în informatică și matematică datorită utilizării lor în diverse aplicații și probleme. Cei mai cunoscuți algoritmi de sortare, la nivel general sunt:
- Bubble Sort – Compara și interschimbă elementele adiacente, trecând repetat prin listă până când aceasta este sortată. Chiar dacă este simplu și ușor de înțeles el este ineficient pentru listele mari.
- Insertion Sort – Inserează fiecare element din lista nesortată în poziția sa corectă din lista sortată cu aceleași avantaje și dezavantaje pentru listele mari ca Bubble sort.
- Selection Sort – Găsește elementul minim din lista nesortată și îl pune la început. Repetă pentru fiecare element.
- Merge Sort – Împarte lista în două jumătăți, sortează fiecare jumătate și apoi le îmbină într-o listă sortată, un pic mai stabil pentru liste mari.
- Quick Sort – Alege un element pivot, împarte lista în subliste cu elemente mai mici și mai mari decât pivotul și sortează recursiv sublistele. Este unul din celele mai eficiente pentru liste mari dar performanța este una redusă.
- Heap Sort – Construiește un heap maxim din listă și apoi extrage elementele unul câte unul pentru a obține lista sortată.
- Counting Sort – Numără numărul de apariții ale fiecărui element și folosește aceste informații pentru a construi lista sortată.
- Radix Sort – Sortează elementele în funcție de cifrele lor, utilizând un sortare stabilă la fiecare pas.
- Bucket Sort – Împarte lista în mai multe segmente, sortează fiecare segment individual și apoi le îmbină.
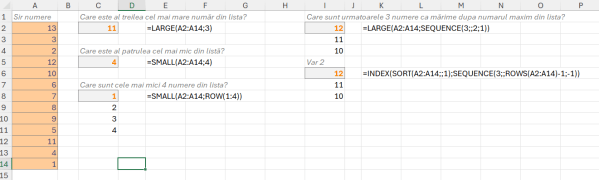
În Excel, în versiunea clasică există doar operațiuni pentru sortare, avantajul major al Excelului modern (365) este faptul că transformă multe operațiuni în funcții. De exemplu avem funcția SORT() sau SORTBY() utilizate pentru sortarea vectorilor. De asemenea, foarte utile sunt funcțiile: UNIQUE() pentru determinarea valorilor unice dintr-un interval precum și funcțiile LARGE() prin intermediul căreia putem identifica cele mai mari n valori dintr-un vector sau funcția SMALL() care ne permite identificarea celor mai mici n valori dintr-un vector.
În imagine câteva detalii legate de utilizarea LARGE și SMALL
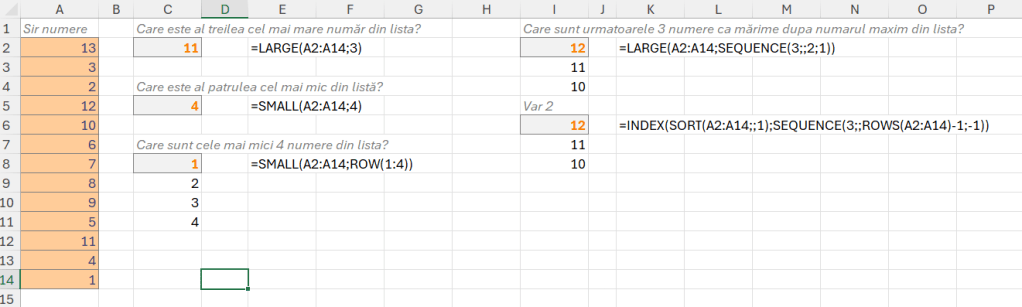
Ca să putem selecta mai multe rânduri dintr-un vector putem utiliza funcția ROW() sau SEQUENCE(). A nu neglija funcția INDEX() care încă este destul de puternică și des utilizată pentru a axtrage valori de pe diferite poziții dintr-un vector.
Problema Distinct
În problema Distinct ni se solicită să determinăm numărul de elemente unice dintr-un vector de valori.
În rezolvarea problemei ar trebui să determinăm fiecare număr unic, să facem un COUNTIF() după fiecare număr pe vectorul de valori după care să însumăm valorile intermediare.
Rezolvarea în Excel este în schimb mult mai simplă:

Așa cum explicam în partea de teorie funcția UNIQUE() îmi determină valorile unice, iar cu COUNT() determin numărul lor. În cazul în care nu avem Excel 365 putem merge pe abordarea din metoda clasică cu însumarea din funcția specificată. Ca să determinăm care sunt exact numerele unice, o tehnică de multe ori necesară în verificarea și validarea seturilor de date atunci putem utiliza combinația de SORT() cu UNIQUE().
Problema MaxProductOfThree
Aceasta este o problemă destul de interesantă a cărei cerință este să determini produsul maxim a trei valori dintr-o listă dată, în care intervalul de valori este negativ și pozitiv. Ca metodă de rezolvare, ar trebui sortat crescător intervalul de valori după care se înmulțesc cele mai mari 3 numere.
Propunere de rezolvare inițială:
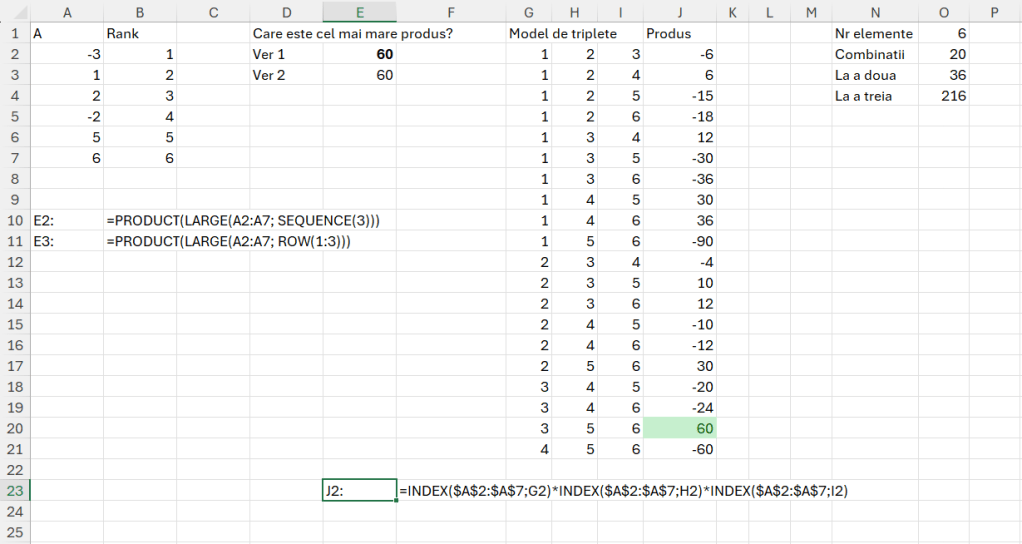
Funcția LARGE() din E2 și E3, preia automat cele mai mari 3 numere din șir fără să fie nevoie de sortare. După care aplicăm funcția PRODUCT() (un fel de SUM() mai puțin utilizat) pentru a înmulți cele 3 numere rezultat. Dezavantajul acestei abordări este că nu pot extrage din rezultat care sunt pozițiile numerelor din RANK decât dacă fac o nouă funcție de căutare pe intervalul de valori.
În zona G:J am încercat o abordare manuală de generare a tuturor combinațiilor posibile unice de la 1 la 6. În cazul în care ai mai multe numere această abordare devine complet ineficientă pentru a fie executată manual. Vezi zona N:O în care sunt explicate în funcție de numărul de elemente, numărul de combinații unice, dar și celelalte combinații, ridicarea la a doua și a treia care determină numărul maxim de combinații pe care le putem obține din numărul de elemente dat.
În J2 am introdus un clasic INDEX() care îmi caută în funcție de tripletă valorile pe vector și le înmulțește între ele, valoarea finală fiind 60 în imputul dat.
Doar că matematica are detaliile ei, pe care dacă nu le verificăm bine riscăm să cădem în capcana datelor de intrare. Se face că în aritmetică, două numere negative când se înmulțesc, obținem un număr pozitiv. Dar numerele negative nu sunt tratate corect cu funcția LARGE() ceea ce înseamnă că ar trebui să complicăm formulele inițiale din E2 ca să conțină și un SMALL() după care să facem un maxim între produsul celor mai mici două numere cu cel mai mare număr, cu produsul celor mai mari 3 numere.

În imagine se observă că modelul manual generează valori corecte, pe când modelul simplu din E2 intoarce doar produsul celor mai mari 3 numere, în cazul meu pozitive.
Având în vedere că o generare manuală a unui tabel de triplete nu este acceptabil de la un anumit număr de valori dintr-un vector, am procedat la implementarea unei funcții separate:

În care funcția concretă este:
=LET(vector; A2:A7;
nr; ROWS(vector);
matrix; MAKEARRAY(nr^3; 3; LAMBDA(i;j; IF(j = 1; INT((i-1)/nr^2)+1; IF(j = 2; MOD(INT((i-1)/nr); nr)+1; MOD(i-1; nr)+1))));
fReq; LAMBDA(x; AND(INDEX(x;1)<INDEX(x;2);INDEX(x;2)<INDEX(x;3)));
verif; BYROW(matrix; LAMBDA(r; fReq(r )));
tabi; HSTACK(matrix; verif);
unics; FILTER(tabi; TAKE(tabi;;-1)=TRUE);
unicsm; CHOOSECOLS(unics;1;2;3);
fReqv; LAMBDA(x; INDEX(vector;INDEX(x;1))*INDEX(vector;INDEX(x;2))*INDEX(vector;INDEX(x;3)));
vals; BYROW(unicsm; LAMBDA(r; fReqv(r )));
MAX(vals))în care variabilele matrix, verif, tabi, unics, unicsm le utilizez doar pentru a crea în mod dinamic tabelul de triplete constând în combinațiile unice pe care le pot lua pozițiile numerelor. Acest tabel îmi este necesar pentru a face ulterior indexul din funcția recursivă fReqv. Funcția o folosesc ulterior în variabila vals pentru a putea să calculez pe tabelul unicsm (tripletele unice) linie cu linie cu BYROW().
La final afișez MAX(vals) pentru a determina care este valoarea maximă a produsului a trei numere din șir.
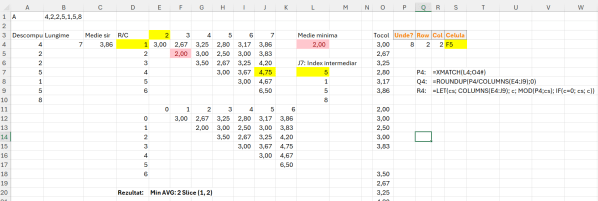
Mi-a fost destul de greu să ajung la formula din matrix. Clar numărul de combinații optime este dat de numărul de elemente din vector, la numărul de elemente combinate. În cazul nostru 3. În schimb pentru a putea determina toate combinațiile posibile, singura metodă pe care am găsit-o este să generez un tabel care are numărul de linii egal cu fiecare număr din șir de câte poziții poate lua pe 3 coloane. De exemplu dacă vectorul A este format din valorile 1, 3, 8, atunci valoarea matrix va cuprinde toate combinațiile lui 1 cu el însăși și cu cu celelalte valori. Exemplificarea din imagine este mult mai concludentă:
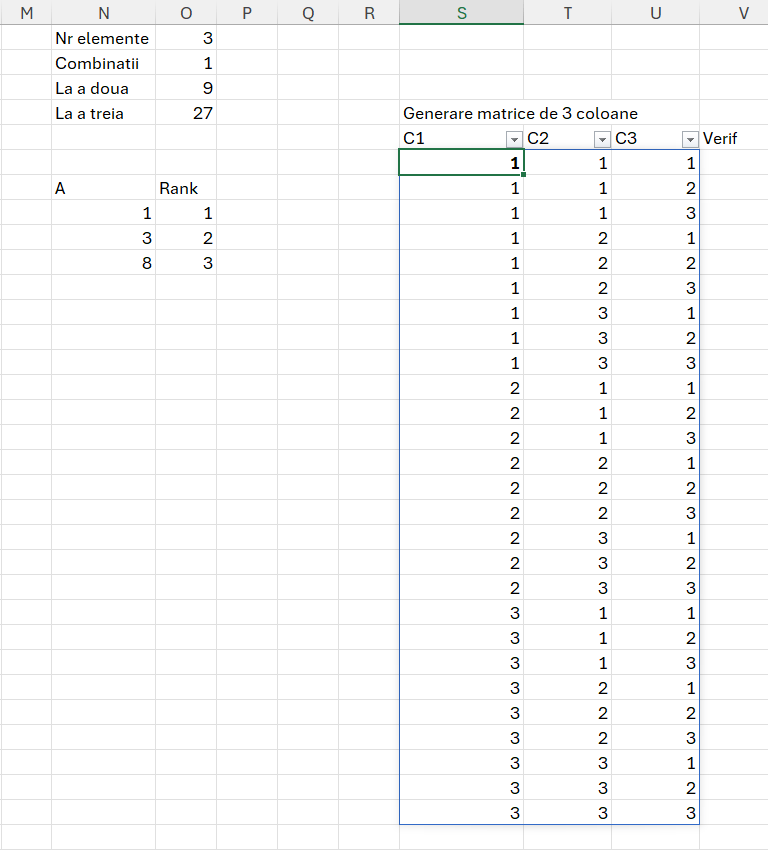
Observăm din imagine că funcția de generare a acestei matrici cuprinde toate valorile posibile. Matricea este doar pentru căutare ulterioară pe A, prin combinația poziției numerelor. Fiecare număr apare de 9 ori pe prima coloană reprezentând numărul de element la puterea a doua. Scopul final este să identific toate combinațiile crescătoare și să elimin duplicatele prin funcțiile următoare. Tabelul final de căutare fiind în variabila unicsm care are un număr de linii egal cu numărul de combinații: 3 combinat cu 3 = 1.

Acest tip de problemă are o mare aplicabilitate în diverse domenii de activitate: analiză financiară, optimizarea producției, logistică, ect cu scopul de a maximiza profitul rezultat în urma activității prin combinarea elementelor optime.
De exemplu, dacă am avea un portofoliu de acțiuni cu diferite randamente, putem calcula combinația maximă dintre ele prin utilizarea funcției propuse:

În funcția de mai sus am înlocuit MAX(vals) cu FILTER(HSTACK(unicsm;vals);vals=MAX(vals)) în așa fel încât să păstrez ca rezultat valorile combinațiilor maxime ca produs.
Un artificiu foarte util pentru a nu ne trezi cu surprize pentru valorile negative, este acela de a transforma procentul în valoare prin adunarea valorii 1 la randament. De exemplu pentru prima valoare formula utilizată este: =1+VALUE(C29). Asta îmi permite să exclud valorile negative din combinație și să păstrez pentru acest caz particular doar valorile pozitive.
Problema Triangle
Problema Triangle este oarecum asemănătoare cu cea anterioară doar că de data aceasta rezultatul nu mai este maximul numerelor ci un rezultat de constatare, dacă 3 numere dintr-un șir pot forma un triunghi. Nu ne referim la cazuri specifice de triunghiuri isoscel, dreptunghic sau echilateral ci doar la cazul în care numerele prezentate (P, Q, R) respectă următoarele reguli:
0<=P<Q<R<N
P+Q>R
Q+R>P
R+P>Q
adică suma oricăror două numere trebuie să fie mai mare decât un al treilea. N reprezintă numărul de elemente din vectorul de analiză. Ca o particularitate a problemei, toate numerele din A trebuie să fie diferite între ele.
Soluția propusă de mine pornește de la funcția de la problema MaxProductOfThree.

Rezultatul este numărul de triplete posibile și care este aceasta. Codul funcției prezentat mai jos:
=LET(vector; A2:A7;
nr; ROWS(vector);
matrix; MAKEARRAY(nr^3; 3; LAMBDA(i;j; IF(j = 1; INT((i-1)/nr^2)+1; IF(j = 2; MOD(INT((i-1)/nr); nr)+1; MOD(i-1; nr)+1))));
fReq; LAMBDA(x; AND(INDEX(x;1)<>INDEX(x;2);INDEX(x;2)<>INDEX(x;3);INDEX(x;1)<>INDEX(x;3)));
verif; BYROW(matrix; LAMBDA(r; fReq(r )));
tabi; HSTACK(matrix; verif);
unics; FILTER(tabi; TAKE(tabi;;-1)=TRUE);
unicsm; CHOOSECOLS(unics;1;2;3);
fReqv; LAMBDA(x; CONCAT(INDEX(vector;INDEX(x;1));";";INDEX(vector;INDEX(x;2));";";INDEX(vector;INDEX(x;3))));
vals; BYROW(unicsm; LAMBDA(r; fReqv(r )));
Split; --TEXTSPLIT(TEXTJOIN("|";1;vals);";";"|");
fverif; LAMBDA(x;AND(INDEX(x;1)+INDEX(x;2)>INDEX(x;3);
INDEX(x;1)+INDEX(x;3)>INDEX(x;2);
INDEX(x;2)+INDEX(x;3)>INDEX(x;1)));
verift; BYROW(Split; LAMBDA(r; fverif( r)));
tabf; HSTACK(Split; verift );
triplef; FILTER(tabf; TAKE(tabf;;-1)=TRUE;"0");
rezfin; IF(ROWS(triplef)>1;"Rezultat: 1 - Tripleta:" & TEXTJOIN(";";TRUE; XMATCH(TAKE(triplef;1;3);vector)-1);"Rezultat: 0");
rezfin)În care tehnica de a obține toate combinațiile unice posibile de poziții din șir este dată de variabilele și funcțiile recursive până la vals. Artificiul esențial în această funcție, este acela de a împărți valorile în LET() prin unificarea inițială a lor din combinația funcțiilor din variabila Split. Această tehnică am învățat-o de la Diarmuid Early fost campion mondial la Excel.
Cheia problemei este în funcția recursivă fverif care este utilizată în BYROW-ul de la verift pentru a compara sumele valorilor din tabelul Split prin adunarea valorilor indexate de pe cele trei coloane. AND()-ul va returna TRUE sau FALSE pe care le unific în tabf cu HSTACK. Ulterior filtrez în triplef doar valorile TRUE din tabf.
Identificarea tringhiurilor dreptunghice
Cred că sunt puțini cei care nu au spus niciodată că anumite formule din matematică nu le folosește la nimic. :) Una din experiențele mele în acest sens cu copiii mei a fost să le demonstrez în nenumărate rânduri utilizatea Teoremei lui Pitagora. Nu am reușit niciodată! :)
Pe scurt în această teoremă, dacă A^2+B^2=C^2 înseamnă că triunghiul este unul dreptunghic (unghi de 90 de grade pentru cei care au uitat).
Ca să identificăm dintr-un șir de valori, care oricare trei numere pot forma un triunghi dreptunghic, am extins problema Triangle descrisă anterior și am modificat funcția recursivă fverif pentru a răspunde noii condiții de sumă a pătratelor.

În zona GHI identificăm numerele din șirul A care pot forma tringhiuri dreptunghice.
3^2+4^2=9+16=25=5^2
5^2+12^=13^2
Funcția utilizată în acest caz este:
=LET(vector; A2:A7;
nr; ROWS(vector);
matrix; MAKEARRAY(nr^3; 3; LAMBDA(i;j; IF(j = 1; INT((i-1)/nr^2)+1; IF(j = 2; MOD(INT((i-1)/nr); nr)+1; MOD(i-1; nr)+1))));
fReq; LAMBDA(x; AND(INDEX(x;1)<>INDEX(x;2);INDEX(x;2)<>INDEX(x;3);INDEX(x;1)<>INDEX(x;3)));
verif; BYROW(matrix; LAMBDA(r; fReq(r )));
tabi; HSTACK(matrix; verif);
unics; FILTER(tabi; TAKE(tabi;;-1)=TRUE);
unicsm; CHOOSECOLS(unics;1;2;3);
fReqv; LAMBDA(x; CONCAT(INDEX(vector;INDEX(x;1));";";INDEX(vector;INDEX(x;2));";";INDEX(vector;INDEX(x;3))));
vals; BYROW(unicsm; LAMBDA(r; fReqv(r )));
Split; --TEXTSPLIT(TEXTJOIN("|";1;vals);";";"|");
fverif; LAMBDA(x;OR(INDEX(x;1)^2+INDEX(x;2)^2=INDEX(x;3)^2;
INDEX(x;1)^2+INDEX(x;3)^2=INDEX(x;2)^2;
INDEX(x;2)^2+INDEX(x;3)^2=INDEX(x;1)^2));
verift; BYROW(Split; LAMBDA(r; fverif( r)));
tabf; HSTACK(Split; verift );
triplef; FILTER(tabf; TAKE(tabf;;-1)=TRUE;"0");
fSort; LAMBDA(row;TEXTJOIN(";";TRUE;SORT(TRANSPOSE(row))));
tabs; BYROW(triplef; LAMBDA(r; fSort(r)));
pita; TEXTSPLIT(TEXTJOIN("|";1;UNIQUE(tabs));";";"|");
pita)În care recunoașteți codul de la problema Triangle cu modificarea specificată pentru fverif, doar că de data aceasta am folosit funcția OR() pentru a identifica oricare din combinațiile dintre cele 3 numere. De asemenea, specific acestei probleme, ca să pot face sortare în LET cu BYROW trebuie să folosim artificiul amintit anterior cu splitarea după join. Funcția recursivă fSort îmi crează un tabel cu toate valorile sortate crescător dar ca să le pot trata am nevoie de ea în BYROW().
Înainte de splitare, variabila tabs are următoarea formă:

În cazul în care șirul de numere nu are valori care să îndeplinească condiția de triunghi dreptunghic, atunci rezultatul returnat va fi zero, ca parte a variabilei triplef.
Problema Triangle poate fi aplicată în diferite domenii de activitate cu efect de optimizare a costurilor, prețurilor sau evaluare a diferitelor riscuri. În analiza pieței imobiliare, algoritmul Triangle poate fi folosit pentru a evalua relațiile dintre prețurile proprietăților în trei locații diferite. De exemplu, dacă prețurile locuințelor în trei cartiere formează un triunghi, se poate evalua dacă aceste prețuri sunt în echilibru sau dacă există anomalii care ar putea sugera oportunități de investiție sau riscuri. În piețele financiare, portofoliile de investiții sunt adesea analizate pentru a evalua riscul și rentabilitatea. Folosind un algoritm Triangle, se pot evalua trei acțiuni sau active diferite pentru a determina dacă formarea lor (în termeni de valori sau randamente) formează un „triunghi” de risc echilibrat. Un portofoliu ideal ar trebui să aibă un echilibru între risc și rentabilitate, iar algoritmul poate ajuta la identificarea combinațiilor care nu sunt optim echilibrate.
În domeniul logisticii, determinarea rutelor optime pentru transportul mărfurilor poate beneficia de algoritmi de tip triunghi. De exemplu, dacă trebuie să transportați mărfuri între trei depozite, algoritmul poate ajuta la determinarea rutei optime care minimizează costurile și timpul, verificând dacă distanțele dintre depozite formează un triunghi optim din punct de vedere logistic. În managementul resurselor umane, performanța angajaților poate fi analizată în grupuri de câte trei pentru a vedea dacă există un echilibru în echipă. Dacă performanța a trei angajați formează un „triunghi”, managerii pot evalua dacă acest triunghi este echilibrat sau dacă există nevoi de formare suplimentară pentru a echilibra performanțele.
Problema NumberOfDiscIntersections
Problema NumberOfDiscIntersections presupune să găsești numărul de perechi de discuri care se intersectează într-un plan 1D. Fiecare disc este definit prin centrul său (o poziție pe axa x) și raza sa (o lungime care se extinde la stânga și la dreapta de la centru).
Discurile sunt date sub forma unui array A, unde fiecare element A[i] reprezintă raza discului centrat în punctul i.
Trebuie să recunosc că problema mi-a dat bătăi de cap, pentru că nu am înțeles de la început cerința. Numărând intersecțiile de pe reprezentarea grafică, luând în calcul și punctele de tangență, tot nu reușeam să ajung la valoarea 11 propusă de autori.
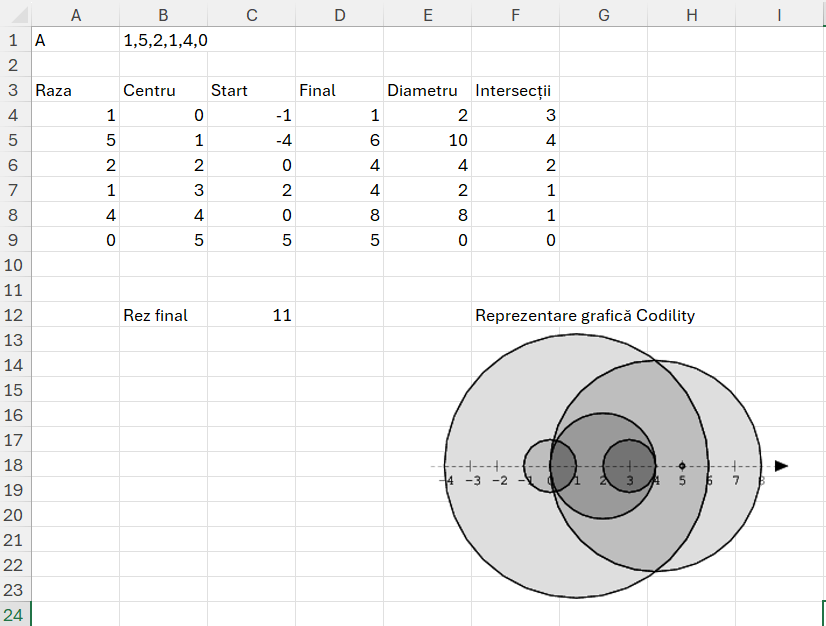
Consultând diferite site-uri specializate am identificat faptul că în această problemă cei de la Codility au luat în calcul de fapt componența fie și parțială a unui disc într-un alt disc. De exemplu discul 5 nu conține nici un alt disc, dar el este numărat ca apartenență atât în discul 1 (cel mai mare cât și în discul 4.
În momentul în care înțelegi că nu este vorba de intersecția liniilor între ele, treaba devine relativ simplă. Eu am rezolvat cu un SUMPRODUCT() comparând valorile de start cu valorile de final și invers, adăugând în ecuație poziția în calcul.
Ca să ajung la rezultat a trebuit să transform comparația fiecărui element cu celălalt element într-o matrice de elemente, artificiul aici fiind funcția TRANSPOSE().
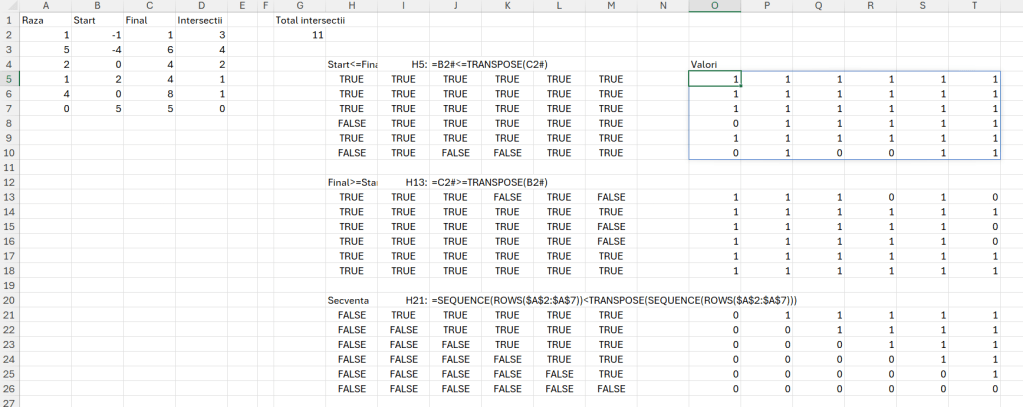
Partea de secvență o folosesc pentru a limita valorile calculate pentru intersecție doar pentru partea în care linia curentă este mai mică decât transpusul său.
După multe chinuri în înțelegerea problemei am ajuns la următoarea funcție:
=LET(sir;B1;
raza;--TEXTSPLIT(sir;;",");
centru;SEQUENCE(ROWS(raza);1;0;1);
start;centru-raza;
final;centru+raza;
tabi;HSTACK(start;final);
tFinal;TRANSPOSE(final);
tStart;TRANSPOSE(start);
intersections;BYROW(tabi;LAMBDA(_;
SUMPRODUCT(
--(start<=tFinal);
--(final>=tStart);
--(SEQUENCE(ROWS(raza))<TRANSPOSE(SEQUENCE(ROWS(raza))))
)
));
MAX(intersections))Din cauză că formula se execută pe un tabel, obțin valoarea 11 pentru fiecare linie din raza. Atunci la final am aplicat funcția MAX() pentru a obține o singură valoare.
În funcția prezentată nu am mai folosit un recursiv, ci am folosit o funcție LAMBDA() cu paramentru null (_) pentru că am input din variabila tabi, ci o folosesc doar pentru a parcuge linie cu linie tabelul inițial.
Nu sunt foarte mulțumit de ce a ieșit, din cauză că am lucrat prea mult la ea, iar unul din princiile mele de lucru în Excel este: Dacă ceva îți ia prea mult timp pentru a găsi o soluție, înseamnă că ceva nu faci bine.
Posibil să existe mai multe metode de aplicare a acestei probleme, dar dacă ne referim la intersecții, cel mai probabil problema ar trebui să ia în calcul amplasamentele pe o hartă care de obicei are coordonate X, Y, nu doar o axă OX ca în această problemă.
Cam atât pentru acest articol! Dacă aveți alte variante de rezolvare vă rog să utilizați secțiunea comentarii. Pentru pasionați vă aștept cu o rezolvare pentru problema intersecției cercurilor în format XY.
Sper să fie util cuiva!

![Problema PassingCars ]n Excel](https://valygreavu.com/wp-content/uploads/2024/05/image-11.png?w=1024)









