Acest articol este mai mult o continuare a articolului cu numere prime Modele de algoritmi în #Excel – Prime and composite numbers (10). Nu prea înțeleg eu ce le plac atât de mult matematicienilor numerele prime, dar eu îmi aduc aminte, fără prea multă nostalgie, despre genul ăla de probleme de la matematică: Demonstrați că 1013 este prim. Jdemii de împărțiri și iar împărțiri. Cred că asta era singura metodă.

În acest articol voi propune o rezolvare pentru problemele de pe site-ul Codility de la această adresă: https://app.codility.com/programmers/lessons/11-sieve_of_eratosthenes/

Dar să continuăm un pic partea de data trecută de ….

Un pic mai multă de teorie

Menționam în articolul anterior că există mai multe metode de a determina dacă un număr este prim sau nu. Prima metodă antică de determinare a numerelor prime este cunoscută sub numele de Ciurul sau Sita lui Eratostene. La informatica de liceu acest algoritm este unul de bază și sunt tot felul de metode de rezolvare. Doar că în Excel nu putem trata valorile viitoare dintr-un vector sau tabel. Orice funcție, chiar dacă este dinamică sau nu, oferă rezultat doar pentru valoarea sau poziția curentă, chiar dacă se poate raporta la toate elementele vectorului sau doar anumite segmente. O funcție dinamică scrie pe tot blocul, fără să poată face iterații de a reveni la un rezultat deja calculat. Odată ce înțelegi asta, realizezi că aplicarea algoritmului lui Eratostene nu prea are aplicabilitate în programarea funcțională în Excel.

Alternativa de a genera toate numerele prime până la un N dat este foarte simplă în Excel.

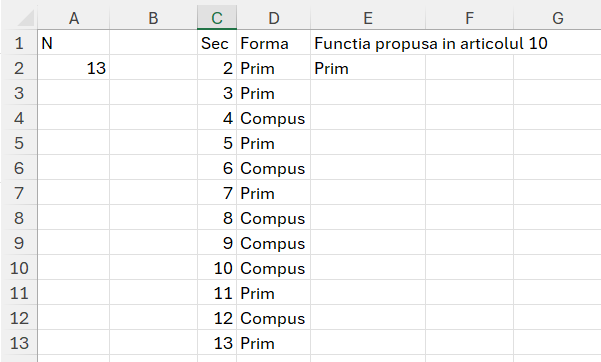
În rezolvarea problemei am utilizat o secvență cu start de la 2 în C2 după care o funcție pentru a calcula pe întreaga secvență fiecare număr prin inpărțire la numerele anterioare. Funcția propusă:

=LET(n; A2;
     arr; C2#;
     freq; LAMBDA(x; LET(arrn; TAKE(arr;x-2);
                         deimpartit; SUM(--(x/arrn-INT(x/arrn)=0));
                        --IFERROR(deimpartit; FALSE)));
    rez; MAP(arr; LAMBDA(v; IF(freq(v)=0;"Prim";"Compus")));
  rez)

în care am definit funcția recursivă freq pe care o apelez în MAP pentru a scana secvența generată în C2#. Variabila deimpartit este cheia în abordare pentru că verifică dacă valoarea curentă (x) împărțită la valorile anterioare arrn obținut prin acel TAKE() minus întregul împărțirii este egal cu zero. Valoarea inițială generează TRUE sau FALSE după caz, după care prin –() transform valorile TRUE, FALSE în 1 și 0 pe care le însumez. Acest artificiu îmi spune în MAP-ul de mai jos dacă numărul este prim sau nu prin raportare la valoarea 0. O nimica toată! :)

Normal metoda propusă este limitată la numărul de linii din Excel. Ca să pot totuși să fac anumite optimizări am încercat să aplic tehnicile din Ciurul lui Atkin, dar îmi dă cu multe virgule. Totuși am studiat un liceu economic și o facultate de contabilitate… nu mă ajută procesorul mai mult. :)

Ca să pot totuși optimiza prin implementarea algoritmului Prim-Dijkstra de raportare la radicalul numărului N dar și o oarecare forțare a ciurului lui Eratostene printr-o mică forma optimizată a lui Atkin de segmentare, plus optimizarea numerelor de verificat prin generare doar de secvențe de numere impare, am ajuns la o matrice pe care o denumesc Matrice de proiecție Eratostene – Dijkstra.

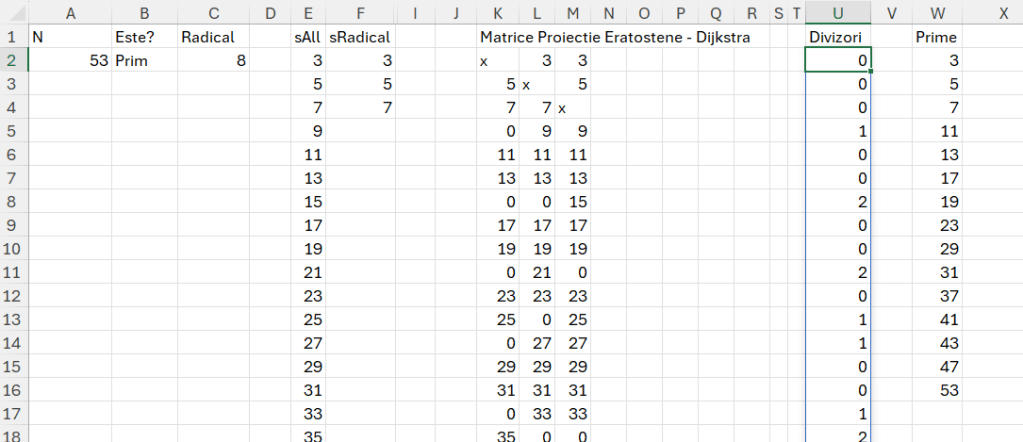
În propunerea am realizat o matrice cu numărul de linii ale sAll care este secvența de numere începând cu 3 și numărul de coloane echivalent radicalului din N-ul dat. Apoi împart fiecare valoare de pe sAll la fiecare valoare de pe sRadical. Funcția de generare a matricei este:

=MAKEARRAY(ROWS(E2#); ROWS(F2#); 
    LAMBDA(r;c; IF(r=c;"x";IF(INDEX(E2#;r)/INDEX(F2#;c)-  
                          INT(INDEX(E2#;r)/INDEX(F2#;c))>0;INDEX(E2#;r);0))))

în care r mă ajută să caut valorile de pe coloana sAll iar c valorile de pe sRadical. În cazul în care s/r sunt egale nu le tratez ci terurnez acel „x”. Dacă apar pe liniile matricei valori 0 înseamnă că acel număr are divizori înaintea sa. În U2 calculez apoi câți de zero sunt pe o linie cu un simplu countif() integrat într-un BYROW: =BYROW(K2#; LAMBDA(r; COUNTIF(r; 0))). Dacă numărul de 0 este 0 acel număr este prim.

Tehnica propusă funcționează destul de bine la valori mici… dar Excelul începe să returneze mesaje de eroaroare că nu poate procesa funcția la N-uri mai mari.

Într-o abordare oarecum mai fabuloasă… de dragul exercițiului am încercat să forțez un SCAN să facă treaba matricei, dar optimul în rulare este tot la numere mici.

Am încercat să abstractizez cât mai mult prin funcții recursive în funcții recursive și merge… dar tot pentru numere mici. În G avem lungimea în caractere a rezultatului. După anumită valoare a lui N nu mai rezultă nimic. Funcția de dragul exercițiului este:

=LET(_s1; E2#; _s2; F2#;
freq; LAMBDA(x;yarr; --(yarr/x-INT(yarr/x)<>0));
ffilter; LAMBDA(xarr;z; FILTER(xarr; freq(z; xarr)=1));
SCAN(""; _s2; LAMBDA(a;v; IF(v=3; TEXTJOIN(";";TRUE;ffilter(_s1; 3)); TEXTJOIN(";";TRUE;ffilter(TEXTSPLIT(a; ;";"); v))))))

SCAN-ul mă ajută să pot păstra rezultatele rulării anterioare, un fel de for cu acumulare… dar cum menționam și în articolele anterioare, SCAN nu returnează tabele, de aceea trebuie păstrate permanent datele concatenate după care le analizăm mai jos splitate. Funcția recursivă freq o folosesc în recursiva ffilter pentru a putea calcula în funcție de valoarea curentă de pe S2 împărțirea a cea a rămas și verificarea dacă este sau nu egală cu 0. ffilter păstrează doar rezultatele cu 1, adică numerele care în rularea anterioară nu au fost deja împărțite.

Până la limitarea de 15 cifre a unui N, ne confruntăm în modelele propuse cu limitarea de 2^20 impusă de numărul de linii Excel sau 2^2*2 dacă aplicăm tehnica doar cu impare.

Satisfăcut de rezultatul cercetării, închei acest pasaj cu un citat din Gabriel Liiceanu: „Trebuie, în tot ce trăiești, să descoperi aurul vieții, nu metalul de rând și nu zgura ei” (detalii … triste aici).

Acestea fiind scrise să trecem la probleme… care sunt mult mai simple decât o expune partea teoretică.

Problema CountNonDivisible

Aceasta este o problemă foarte simplă: Dacă ai un array A de N numere întregi, pentru fiecare element A[i], trebuie să determinăm câte dintre celelalte elemente din array nu sunt divizibile cu A[i].

Rezolvarea problemei:

În partea de proiecție am făcut o verificare dacă numărul 3 se împarte la oricare din valorile de pe vectorul A. În cazul în care este divizibil, restul este 0, ceea ce mă ajută să filtrez apoi în C2 calorile care sunt mai mari ca 0.

Integrată soluția este obținută prin funcția:

=LET(a; A2:A7;
     freq; LAMBDA(x; x/a-INT(x/a));
     MAP(a; LAMBDA(v; TEXTJOIN(", ";;FILTER(a; freq(v)<>0; "x")))))

în care recursiva face ce se întâmplă pe coloana B pentru fiecare x de pe A pe care-l parcurg cu MAP. Ca să pot returna valori pentru fiecare linie a trebuit să integrez în lambda acel TEXTJOIN().

Aplicabilitatea acestei probleme cred că ar fi în analiza de piață.

Problema CountSemiprimes

Semiprim este un numar rezultat din produsul a doua numere prime, nu neaparat distincte. Problema cere calcularea numărului de semiprime pentru un N dat și care se află în anumite intervale de valori P, Q specificate.

Propunere de rezolvare

Am numărul N = 26. Calculăm întâi prin metodele specificate numerele prime până la 26. După care calculăm matricea de semiprime, care este rezultatul înmulțirii fiecărui număr prim cu oricare din celelalte. Valoarea semiprimului nu trebuie să fie mai mare ca N.

Pentru asta în H7 am implementat următoarea funcție:

=LET(prime;C2#;
     rr;ROWS(prime);
     matrice; MAKEARRAY(rr; rr;
          LAMBDA(r;c; IF(INDEX(prime;r)*INDEX(prime;c)>A2; "";   
                        INDEX(prime;r)*INDEX(prime;c))));
coli; SORT(UNIQUE(TOCOL(matrice;3))); matrice)

în care utilizez numerele prime rezultate în vectorul C2# după care cu MAKEARRAY indexez fiecare număr și îl înmulțesc cu fiecare. Variabila finală este de fapt coli care transformă matricea într-un vector (TOCOL) de cu valori unice sortate crescător. Valoarea lui coli este în F7.

În J2 calculez apoi cu COUNT numărul de elemente care se regăsesc între P și Q dat. Funcția din J2:

=COUNT(FILTER($F$7#;($F$7#>=H2)*($F$7#<=I2);""))

este de fapt o filtrare cu dublă condiție care returnează un număr de linii. Dacă nu se îndeplinește condiția returnează nimic „”.

Și cam asta este rezolvarea. Simplu și rapid!

Cam atât pentru astăzi!

Sper să vă fie util!