De data aceasta mi-a dat greu! :) De aceea am decis să împart articolul despre numerele Fibonacci în două părți: una pentru problema FibFrog și a doua pentru Ladder. Pentru cititorii care au reușit să urmărească aceste serii complicate de programare funcțională în Excel, poate au observat că în articole sunt vehiculate permanent aceleași funcții, doar cu construcții și cazuri de utilizare diferite.
Pentru acest articol vă propun o metodă de rezolvare a problemei FibFrog de pe site-ul Codility: https://app.codility.com/programmers/lessons/13-fibonacci_numbers/. Trebuie știut că la data publicării acestui articol, nici un instrument de AI nu poate rezolva problema corect în Excel.
Să începem ca de obicei cu …
Un pic de teorie
Sunt foarte multe materiale de studiu pentru numerele Fibonacci pe Internet, ele stârnind interesul multor autori datorită aplicabilității pe scară largă a acestei secvențe.
Secvența Fibonacci este o succesiune recursivă definită de relația de recurență:
F(n)=F(n−1)+F(n−2)
unde F(0)=0 și F(1)=1. Aceasta are multiple aplicații în informatică, inclusiv în algoritmi de optimizare, structuri de date (heap Fibonacci), analiza complexității algoritmilor (divide et impera) și generarea de chei criptografice. Secvența este, de asemenea, utilizată în probleme de programare dinamică și este strâns legată de numărul de aur, având proprietăți logaritmice utile în analiza complexității algoritmilor.
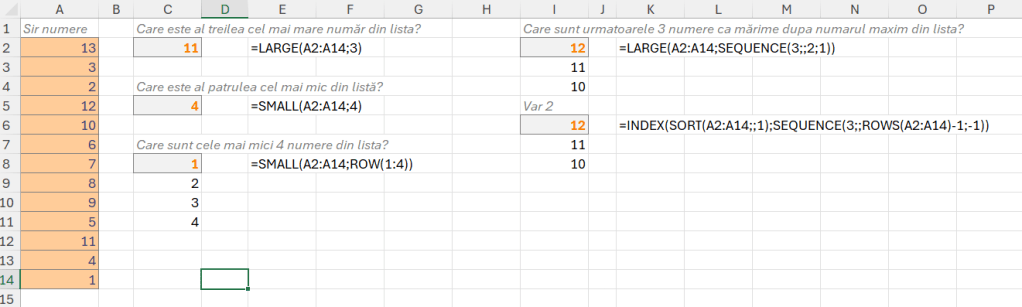
Una din cele mai interesante metode de a calcula șirurile de numere este dată de formula:

Pentru a implementa această formulă în Excel utilizăm cu precădere funcția SQRT() pentru calculul radical și SEQUENCE() pentru valoarea lui n.

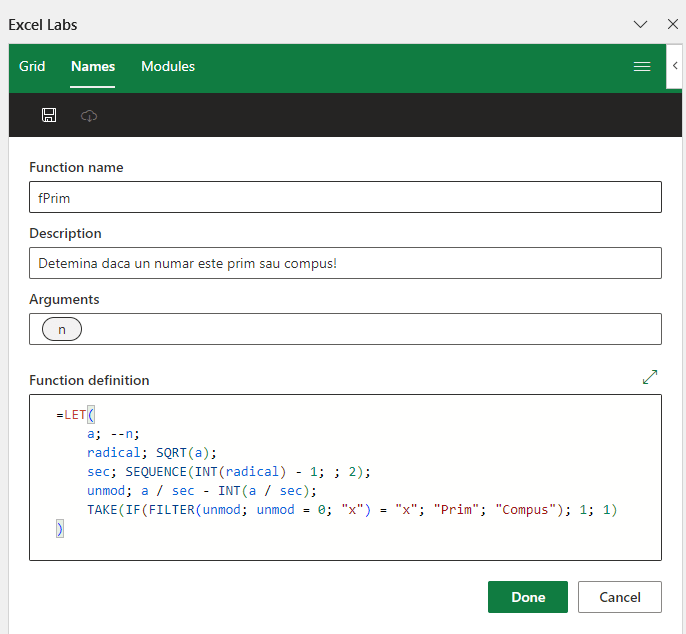
Având în vedere că în rezolvarea problemei am nevoie permanentă de această construcție introduc în acest articol funcția _fFibonacciSir() cu parametrul N pe care o voi reutiliza ulterior.
=LAMBDA(n; DROP((((1 + SQRT(5)) / 2) ^ SEQUENCE(n) - ((1 - SQRT(5)) / 2) ^ SEQUENCE(n)) / SQRT(5); 1))Funcția DROP o utilizez pentru a elimina prima linie din șir, în așa fel încât să rămân cu o singură valoare 1 în rezultat.
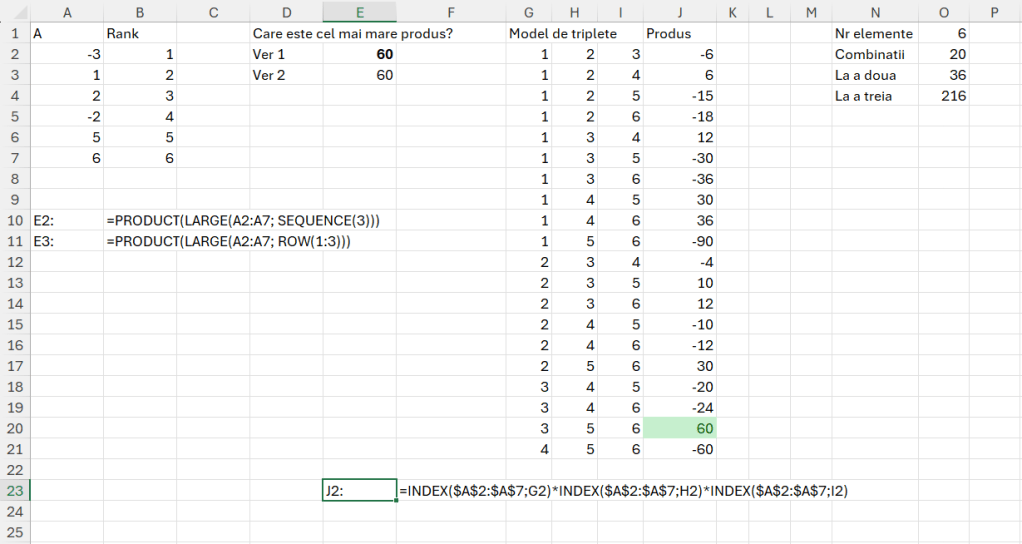
În același timp o variație a acestei probleme este verificarea dacă un număr face parte dintr-un șir Fibonacci. Pentru a rezolva acest aspect introduc funcția _fFibonacciIS() cu paramentrul N, în care N este oricare număr natural pe care doresc să-l testez.
=LAMBDA(n; LET(_n; n; sir; _fFibonacciSir(_n+1); IF(ISNUMBER(MATCH(_n; sir;0)); TRUE; FALSE)))Această funcție returnează valorile TRUE sau FALSE și reutilizează funcția _fFibonacciSir() pentru a calcula secvențele lui N. construcția _n1+1 din parametrul funcției este pentru a corecta problemele numerelor mici: 0, 1. În rezolvarea problemei 0 nu este considerat parte a acestei secvențe, chiar dacă în realitate el este primul număr. În versiunile viitoare voi aduce corecții dar în rezolvarea problemei am nevoie ca 0 să nu fie luat în seamă.
Un alt aspect important în aceste șiruri este raportul sau numărul de aur denumit φ (phi). Acest raport este întâlnit frecvent în lumea care ne înconjoară. Valoarea lui după al 14 element al șirului este 1,61803.
Problema FibFrog sau Salturile Fibonacci prin matrice
Fără a insista pe idioțeniile politice care spamează rețelele sociale, matricile în Excel au o putere deosebită de calcul vectorial și reprezintă o cale elegantă de a rezolva diferite tipuri de probleme.
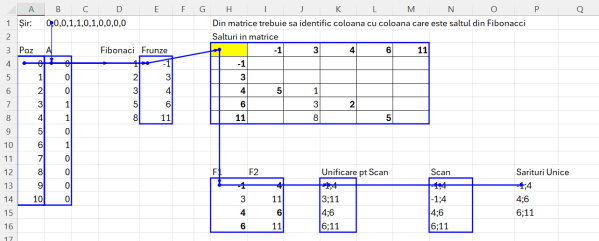
FibFrog este o problemă care combină elemente din teoria numerelor (șirul Fibonacci) și grafuri. Scopul este să determini numărul minim de sărituri pe care o broască trebuie să le facă pentru a traversa un râu reprezentat de o serie de frunze și apă. Avem un șir binar A (de exemplu, [0, 1, 0, 0, 0, 1, 0]), unde: 1 reprezintă o frunză și 0 reprezintă apă. Broasca poate sări doar pe frunze (pe pozițiile marcate cu 1).
Dificultatea problemei este dată de restricția că lungimile săriturilor sunt restricționate la valor care aparțin șirului Fibonacci (F), adică {1, 2, 3, 5, 8, ...}.
Broasca începe la poziția -1 (deci înainte de prima frunză) și trebuie să ajungă după ultima poziție a șirului (pe N, unde N este lungimea șirului). Obiectivul principal este calcularea numărului minim de sărituri necesare pentru a traversa complet șirul de frunze și apă.
Dacă broasca nu poate traversa folosind sărituri din șirul Fibonacci, rezultatul trebuie să fie -1. Pentru a înțelege mai bine problema, cele mai bune explicații le-am găsit în sursa de mai jos.

Sursa: Captură video Youtube: Fibonacci Frog Jump in Python and C++ Codility Coding Interview
Rezolvarea problemei în Excel pas cu pas.

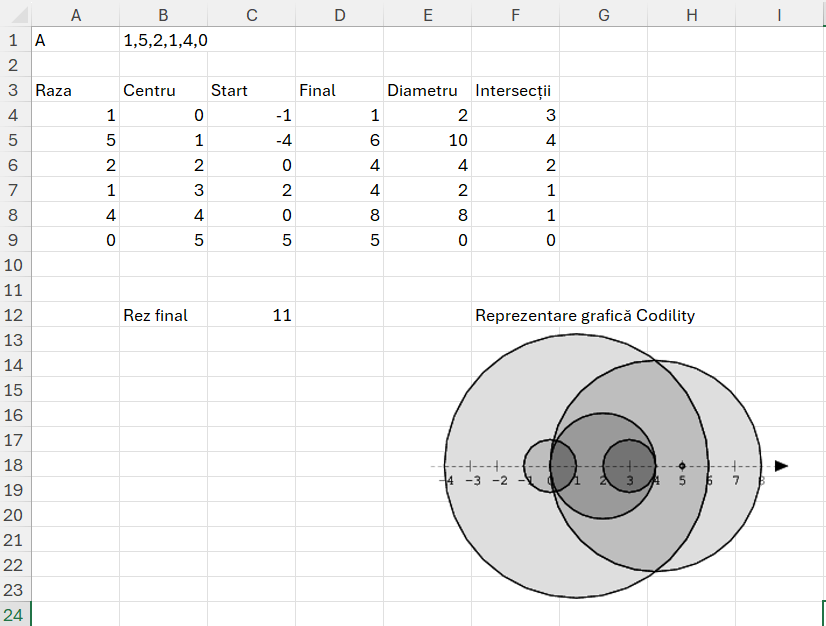
În B4 am descompus șirul dat în B2 cu funcția: =–TEXTSPLIT(B1;;”,”) apoi în A4 am calculat secvența de poziții a fiecărei frunze cu start de la 0: =SEQUENCE(ROWS(B4#);;0)
În D4 am calculat secvența de numere corespondent pozițiilor din A4 prin reutilizarea funcției _fBibonacciSir() definită anterior. M-am raportat la numărul maxim de poziții și am filtrat doar numerele care răspund criteriului: =LET(fib; _fFibonacciSir(MAX(A4#)); FILTER(fib; fib<=MAX(A4#)))
În E4 am calculat poziția frunzelor prin filtrarea vectorului Poz din A4 cu valorile 1 de pe vectorul A din B4. Ca să răspund cerințelor problemei, am adugat valoarea -1 ca fiind malul de start și valoarea maximă din poziții ca fiind malul destinație. =VSTACK(-1;FILTER(A4#;B4#=1);MAX(A4#)+1). În VSTACK() am adăugat 3 termen: valoarea -1, valorile filtrate din poziții și maxim poziții +1.
Cheia problemei este în H3 unde am proiectat o matrice RxC în care antet de coloane și linii sunt valorile frunzelor rezultate în E4. Formula utilizată este:
=LET(arr; E4#; _rows; ROWS(arr);
diff; MAKEARRAY(_rows;_rows; LAMBDA(r;c; IF(c>=r; "";INDEX(arr;r)-INDEX(arr;c))));
fScanCol; LAMBDA(c; MAP(c; LAMBDA(v; IF(_fFibonacciIS(v); v; ""))));
fin; VSTACK(HSTACK(""; TRANSPOSE(arr));HSTACK(arr; fScanCol(diff)));
fin)în care un rol deosebit îl are funcția recursivă fScanCol care apelează funcția creată anteriror: _fFibonacciIS(). Rolul său este de a păsta în matrice doar valorile din șirul Fibonacci.
Variabila diff este utilizată pentru a genera matricea ințială prin care scad valorile corespondente din vectorul arr pe toate combinațiile posibile. Ca să pot afișa antetele matricei (linii și coloane) am folosit o combinație de VSTACK() cu HSTACK().
A doua cheie este în H13 unde am extras toate combinațiile optime de salturi.
=LET(tab;H3#;_hr;CHOOSEROWS(tab;1);_hc;CHOOSECOLS(tab;1);
tabi;SCAN(0;_hc; LAMBDA(a;v;LET(colc;XMATCH(v;_hr;0);
poz;XMATCH(1;--ISNUMBER(CHOOSECOLS(tab;colc));0;-1);
valc;INDEX(_hr;poz);
return;CONCAT(v;";";valc);
return)));
valori;DROP(DROP(tabi;1);-1);
splited; --TEXTSPLIT(TEXTJOIN("|";;valori);";";"|");
splited)Chiar dacă pare complicată, formula nu face decât să aducă valorile din antetul de linie și coloană specifice valorilor rezultat de pe fiecare coloană. Cheia este valoarea -1 din variabila poz care caută valoarea specifică de jos în sus pe vector-ul _hc care este de fapt prima coloană din matrice. colc este un artificiu care rulează scan-ul în matrice de fapt, coloană cu coloană. Nu aveam cum să rulez funcția BYCOL() pentru că nu o pot integra în SCAN(). Ca să păstrez doar pozițiile în forma start;final am utilizat două funcții DROP() prin care am eliminat prima și ultima linie din rezultat. Ca să pot vedea valorile tabelar am implemententat variabila splited care folosește artificiul de splitare linie cu linie.
Rezultatul final al funcției din H13 este identic cu cel din K13, unde am făcut de fapt reunificarea pentru a putea parcurge aceste valori cu scopul de a le extrage pe cele care îndeplinesc criteriul cerut.
Aparent cea mai grea chestie a fost să găsesc calea de a scoate doar perechile corecte de salturi. Pentru asta am încercat diferite abordări dar în final am ajuns tot la un SCAN() pe care l-am implementat în N13:
=SCAN(""; K13#; LAMBDA(a;v; IFERROR(IF(AND(a=""; ISNUMBER(TAKE(--TEXTSPLIT(v;";");;-1)));v; IF(TAKE(--TEXTSPLIT(v;";");;1)=TAKE(--TEXTSPLIT(a;";");;-1);v;a));-1)))În această formulă parcurg vectorul K13# și descompun fiecare valoare F1-F2 pentru a o compara cu cele anterioare. Acumulatorul (a) este reprezentat permanent de combinația câștigătoare anterioară. Dacă valoarea de pe prima combinație nu este un număr atunci rezultatul funcției este -1 așa cum cere problema.
Toate funcțiile și calculele intermediare integrate vor duce la formula finală:
=LET(sir; B1; _A; --TEXTSPLIT(sir;;","); poz; SEQUENCE(ROWS(_A);;0);
fReqFS; LAMBDA(n; DROP((((1 + SQRT(5)) / 2) ^ SEQUENCE(n) - ((1 - SQRT(5)) / 2) ^ SEQUENCE(n)) / SQRT(5); 1));
fReqFIS; LAMBDA(n; LET(_n; n; sir; fReqFS(_n+1); IF(ISNUMBER(MATCH(_n; sir;0)); TRUE; FALSE)));
fibo; LET(fib; fReqFS(MAX(poz)); FILTER(fib; fib<=MAX(poz)));
frunze; VSTACK(-1;FILTER(poz;_A=1);MAX(poz)+1);
matrix; LET(arr; frunze; _rows; ROWS(arr);
diff; MAKEARRAY(_rows;_rows; LAMBDA(r;c; IF(c>=r; "";INDEX(arr;r)-INDEX(arr;c))));
fScanCol; LAMBDA(c; MAP(c; LAMBDA(v; IF(fReqFIS(v); v; ""))));
fin; VSTACK(HSTACK(""; TRANSPOSE(arr));HSTACK(arr; fScanCol(diff)));
fin);
perechi; LET(tab;matrix;_hr;CHOOSEROWS(tab;1);_hc;CHOOSECOLS(tab;1);
tabi;SCAN(0;_hc; LAMBDA(a;v;LET(colc;XMATCH(v;_hr;0);
poz;XMATCH(1;--ISNUMBER(CHOOSECOLS(tab;colc));0;-1);
valc;INDEX(_hr;poz);
return;CONCAT(v;";";valc);
return)));
valori;DROP(DROP(tabi;1);-1);
valori);
pok; SCAN(""; perechi; LAMBDA(a;v; IFERROR(IF(AND(a=""; ISNUMBER(TAKE(--TEXTSPLIT(v;";");;-1)));v; IF(TAKE(--TEXTSPLIT(v;";");;1)=TAKE(--TEXTSPLIT(a;";");;-1);v;a));-1)));
unice; UNIQUE(pok);
"Nr perechi: " & ROWS(unice)& ": "&TEXTJOIN(" | ";;unice)
)în care nu am mai folosit funcțiile definite la început ci le-am introdus ca recursive în această formulă pentru a evita erorile de a nu avea funcțiile definite / salvate.
Cam atât pentru această parte. Voi reveni cu un video pas cu pas pentru explicații suplimentare și cu partea a doua în viitor.
Aici varianta video pas cu pas.
Sper că v-a plăcut! :)