A trecut ceva vreme de când nu am mai scris pe această temă, mai concret câteva luni de când am scris propunerea de rezolvare pentru Ciurul lui Eratostene. Modele de algoritmi în #Excel – Sieve of Eratosthenes (11)
În acest articol voi propune o rezolvare pentru problemele de pe site-ul Codility de la această adresă: https://app.codility.com/programmers/lessons/12-euclidean_algorithm/
Având în vedere că nu am prea multă teorie nu mai facem o secțiune separată pentru această componentă. Amintim doar că Algoritmul Euclidean este utilizat pentru calcularea celui mai mare divizor comun (GCD) al două numere printr-un proces iterativ sau recursiv de împărțiri succesive; însă, în combinație cu alte metode, poate ajuta la testarea primalității sau la factorizarea numerelor. Detalii foarte faine despre algoritm găsiți la adresa: https://ro.wikipedia.org/wiki/Algoritmul_lui_Euclid
Problema ChocolatesByNumbers
Ai N bucăți de ciocolată aranjate într-un cerc. Numeri aceste bucăți de la 0 la N-1. Începi să mănânci bucăți de ciocolată de la bucata numerotată 0. După ce mănânci o bucată, sari peste M bucăți și mănânci următoarea (adică sari la bucata 0 + M mod N, și tot așa).
Întrebarea este: Câte bucăți de ciocolată vei mânca în total până când te întorci la o bucată pe care ai mai mâncat-o înainte?
Parametrii:
- N: Numărul total de bucăți de ciocolată (N ≥ 1).
- M: Numărul de bucăți peste care sari după ce mănânci o bucată (M ≥ 1).
Exemplu:
Să considerăm cazul în care:
- N = 10 (ciocolată aranjată în cerc cu 10 bucăți)
- M = 4 (sari peste 4 bucăți după ce mănânci una)
Secvența bucăților mâncate va fi: 0 → 4 → 8 → 2 → 6 → 0. Vei mânca 5 bucăți de ciocolată înainte să te întorci la bucata 0.
Observații:
- Vei mânca fiecare bucățică o singură dată înainte de a reveni la o bucățică deja consumată.
- Problema are o legătură cu cel mai mare divizor comun (GCD) dintre N și M.
Rezolvare în Excel

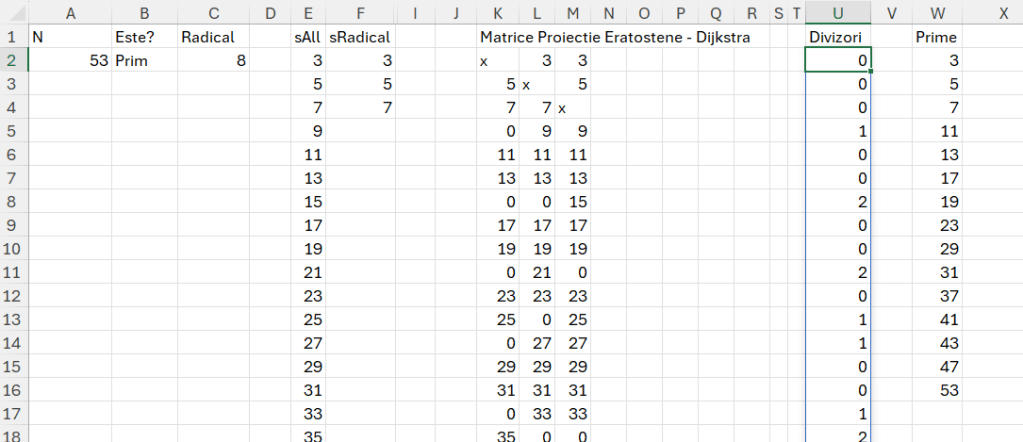
Pas cu pas în rezolvarea problemei, concret începem de la C5 care calculează restul împărțirii numărului N la secvența de numere componente. În felul acesta pentru valorile 0 identificăm divizorii. Procedăm la fel pentru numărul M în celula D5. Ca să aflăm divizorii filtrăm secvența de numere componente pentru toate valorile 0. În felul acesta obținem în E5 si F5 divizorii celor două numere. În G5 căutăm cel mai mare număr comun din cele două șiruri după care indexăm lista divizorilor cu valoarea rezultat și obținem astfel valoarea 2. În context în I5 calculăm numărul N împărțit la cel mai mare divizor comun.
Nu mi-a luat foarte mult timp rezolvarea, dar am fost oarecum dezamagit de mine când am aflat că în Excel există built-in funcția GCD() care returnează exact valoarea mea din H5. În același timp funcția GCD() permite calcularea divizorului comun al mai multor numere. Toată problema se rezumă acum la formula:
=A2/GCD(A2;B2)
De multe ori spun că dacă nu suntem suficient de bine pregătiți riscăm să pierdem foarte mult timp reinventând roata… în cazul acesta roata pătrețelelor de ciocolată. :)
Exemple practice?
Problema se aplică cu succes rezolvării tuturor problemelor ciclice: planificarea reviziei unor mașini de pe un lanț de producție sau în vânzări, planificarea campaniilor de marketing sau promoțiilor specifice.
Problema CommonPrimeDivisors
Această problemă face parte tot din categoria problemelor care implică divizori comuni și numere prime. Scopul acestei probleme este de a determina dacă două numere împărtășesc aceiași divizori primi.
Avem doi vectori de numere întregi, A și B, ambele de lungime N. Pentru fiecare pereche de numere A[i] și B[i], trebuie să verifică, dacă aceștia au exact aceiași divizori primi. Dacă da, se returnează valoarea 1 pentru acea pereche, iar dacă nu returnăm valoarea 0. Rezultatul final este numărul total de perechi de numere care au aceiași divizori primi.
Parametrii:
- A și B: doi vectori de lungime N cu numere întregi pozitive.
Exemplu:
Să presupunem că:
- A = [15, 10, 9]
- B = [75, 30, 5]
Analiza pentru fiecare pereche:
- Pentru A[0] = 15 și B[0] = 75:
- Divizorii primi ai lui 15 sunt 3 și 5.
- Divizorii primi ai lui 75 sunt 3 și 5.
- Cei doi au exact aceiași divizori primi → răspunsul este 1.
- Pentru A[1] = 10 și B[1] = 30:
- Divizorii primi ai lui 10 sunt 2 și 5.
- Divizorii primi ai lui 30 sunt 2, 3 și 5.
- Aceștia nu au exact aceiași divizori primi → răspunsul este 0.
- Pentru A[2] = 9 și B[2] = 5:
- Divizorii primi ai lui 9 sunt 3.
- Divizorii primi ai lui 5 sunt 5.
- Nu împărtășesc aceiași divizori primi → răspunsul este 0.
Rezultatul final al problemei este 1 pentru vă avem o singură pereche care împarte aceeași divizori primi.
Rezolvare în Excel
Ca să putem rezolva un pic mai simplu și mai rapid propun două funcții noi, ca rezultat al cercetărilor din articolele anterioare.
Funcția fPrim() – calculează dacă un număr este prim sau compus. Pentru managementul numelor și funcțiilor eu folosesc Excel Labs, un proiect Microsoft Garage.
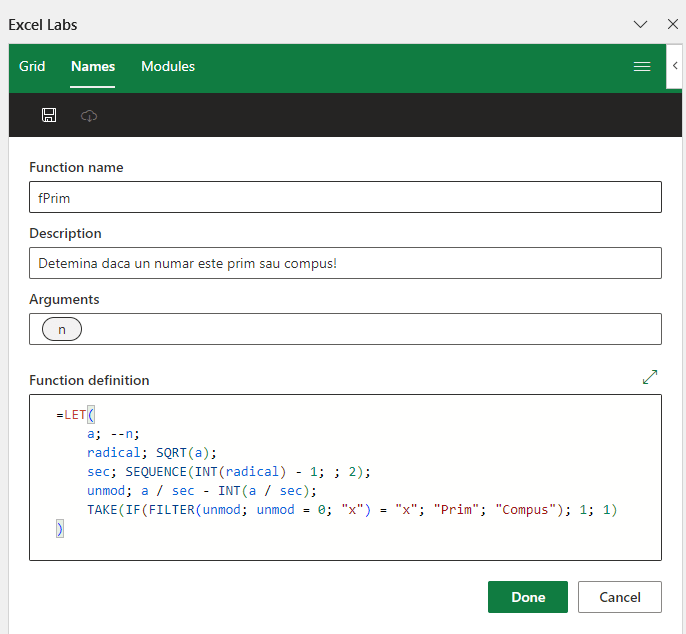
Textul funcției:
=LAMBDA(n; LET(
a; --n;
radical; SQRT(a);
sec; SEQUENCE(INT(radical) - 1; ; 2);
unmod; a / sec - INT(a / sec);
TAKE(IF(FILTER(unmod; unmod = 0; "x") = "x"; "Prim"; "Compus"); 1; 1)
))Funcția are parametrul n care este numărul pe care dorim să-l verificăm. După care se calculează radicalul din acest număr și se realizează un secvență din 2 în 2 a valorilor rezultat. După care calculăm un fel de mod în variabila unmod prin care aflăm restul pe secvențe întregi.
Funcția fPrime() – care determină toate valorile prime de la 2 până la un anumit număr specificat.
=LAMBDA(x; LET(_n; x; toate; VSTACK({2;3};SEQUENCE(_n/2;;5;2));
ftPrim; LAMBDA(n; LET(
a; --n;
radical; SQRT(a);
sec; SEQUENCE(INT(radical) - 1; ; 2);
unmod; a / sec - INT(a / sec);
TAKE(IF(FILTER(unmod; unmod = 0; "x") = "x"; "Prim"; "Compus"); 1; 1)
));
test; MAP(toate; LAMBDA(v; IF(v<5;"Prim";ftPrim(v))));
prime; FILTER(toate;test="Prim"); prime))în această funcție nu am reiterat fPrime() descris anterior ci am făcut o variabilă recursivă ftPrim care înglobează textul funcției. În această funcție pornesc secvența generată de la 5 la care concatenez valorile 2 și 3 cu ajutorul funcției VSTACK{} în așa fel încât să am șirul complet de la 2 încolo.
Rezolvarea problemei în Excel
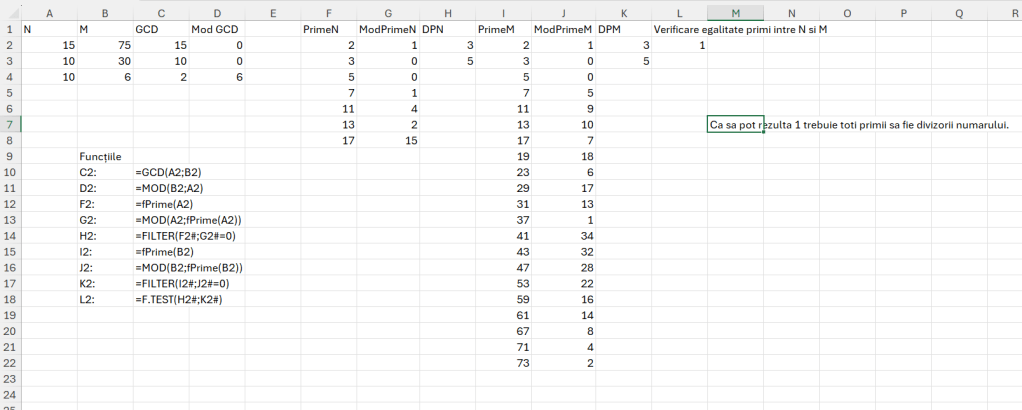
Rezolvarea aceasta este pentru prima pereche de numere.
În C2 determinăm cel mai mare divizor comun, apoi în D2 calculăm restul împărțirii la cele două numere. În F2 și I2 aplicăm funcția fPrime() descrisă anterior pentru a calcula toate numerele prime de la 2 la numărul N și M, iar pentru fiecare din ele calculăm restul împărțirii numărului N și M la numerele prime rezultate, obținând astfel valorile 0 pentru divizori, după care filtrez cei doi vectori rezultat în H2 și K2.
La final pentru perechea 1 dată aplic funcția F.TEST() descrisă în articolul: Excel – Compararea a două coloane cu F.TEST()
Dacă cele două rezultate sunt egale obțin valoarea 1. Dacă nu obțin o valoare între 0 și 1. Pentru valorile date tabelul rezultat este format din valorile. Ceea ce înseamnă că numărând valorile 1 vom obține o singură valore.
1
0,598701901
0,409665529
Funcția finală integrată pentru a rezolva această problemă:
=LET(tab; A2:B4;
rez; BYROW(tab; LAMBDA(r; LET(_n; TAKE(r;;1); _m; TAKE(r;;-1); vGCD; GCD(_n;_m); vMod; MOD(_m;_n);
PrimeN; fPrime(_n); ModPrimeN; MOD(_n; PrimeN); DPN; FILTER(PrimeN; ModPrimeN=0);
PrimeM; fPrime(_m); ModPrimeM; MOD(_m; PrimeM); DPM; FILTER(PrimeM; ModPrimeM=0);
F.TEST(DPN; DPM))));
SUM(--(rez=1))
)Cam asta ar fi pentru astăzi. Sper să fie util cuiva!