După articolul publicat anterior, Modele de algoritmi în #Excel – Binary search algorithm (14), am primit mai multe mesaje de la cititorii acestei serii de articole că problema NailingPlanks returnează foarte puține valori corecte sau optime.

De fapt nu am primit nici un mesaj, decât de la un mic pitic din minte care-mi spunea tot timpul că ceva nu e obine. :) Așa că am luat-o muncitorește de la capăt într-o nouă abordare.

Prima dată, pix și foaie și proiecția problemei! Clar în imagine numărul optim de cuie pentru a fixa toate cele 4 scânduri pe o placă este utilizarea cuielor din poziția 5 și poziția 9. Cuiul 5 prinde scândura 1 și 2 iar cuiul 9 prinde scândura 3 și 4.

Proiecția problemei în Excel

Drumul către o soluție optimă a fost destul de complicat pentru că optimizarea este complexă în sine în orice domeniu.

Ca noutate pentru acest articol a fost să vă pun la dispoziție fișierul cu funcțiile pentru a identifica alte cazuri particulare de probleme care pot apărea în optimizare. Fișierul cu funcția poate fi descărcat de aici.

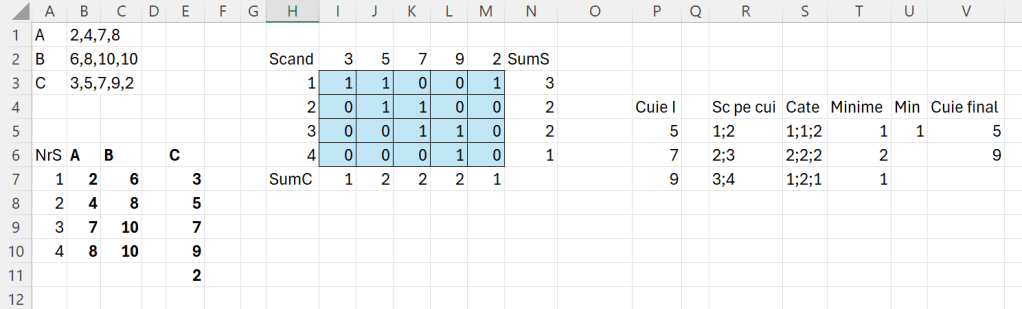
Abordarea a fost să verific dacă fiecare valoare C este cuprinsă în intervalul A-B. Acest lucru se poate face simplu cu o funcție AND() pe care am scris-o în I3. Acesta este de fapt o matrice pe care o vom vedea în funcția finală. Formula din I3: =–AND(I$2>=$B7;I$2<=$C7)

Apoi am calculat suma tuturor intersecțiilor pentru a vedea cate scânduri prinde un cui (SumC) și cate cuie sunt pe o scândură (SumS).

În P5 am realizat o filtrare a tuturor cuielor care sunt candidate pentru optim. Funcția este foarte dinamică soluția pentru a construi este utilizarea repetitivă de funcții de căutare: INDEX(), FILTER(), XMATCH(), cheia fiind dată de dinamizarea liniei pe care se face căutarea prin funcția CHOOSEROWS().

Ulterior în R5 am calculat care scânduri sunt pe fiecare cui iar în S5 am calculat minimul de de căutări ale scândurilor în celelalte valori. De exemplu pentru valoarea 1, scândura apare o singură dată, iar pentru scândura 2 aceasta apare de 2 ori în rezultatele intermediare din R5. Pe baza de minime, am identificat că acele cuie care au o valoare minimă nu pot fi excluse din rezultat. de aceea în V9 am păstrat toate valorile care îndeplinesc criteriul de minim.

Ca să fie frumos am integrat pas cu pas toată funcția în B15, care arată cam în felul următor:

=LET(_a; --TEXTSPLIT(B1;;","); _rows; ROWS(_a);
     _b; --TEXTSPLIT(B2;;",");
     _c; --TEXTSPLIT(B3;;","); _rowc; ROWS(_c);
     matrix; MAKEARRAY(_rows;_rowc; LAMBDA(r;c; --AND(INDEX(_c;c)>=INDEX(_a;r);INDEX(_c;c)<=INDEX(_b;r))));
     scand;SEQUENCE(_rows);
     sums;BYROW(matrix;SUM);
     cuie;TRANSPOSE(_c);
     sumc;BYCOL(matrix;SUM);
     cuiei; LET(
                resulti; MAP(scand;LAMBDA(v;IF(INDEX(sums;v)=0;
                     "Incomplet";
                        IF(INDEX(sums;v)=1;
                        INDEX(cuie;;XMATCH(1;CHOOSEROWS(matrix;v);0));
                             LET(cautCuie;TRANSPOSE(FILTER(cuie;CHOOSEROWS(matrix;v)=1));
                                 cateSc;INDEX(sumc;;XMATCH(cautCuie;cuie));
                                 sortc; SORT(HSTACK(cautCuie; cateSc);2;-1);
                                 TAKE(sortc;1;1)
                        ))))); UNIQUE(resulti)
             );
     scpecui; MAP(cuiei;LAMBDA(v;TEXTJOIN(";";TRUE;FILTER(scand;CHOOSECOLS(matrix;XMATCH(v;cuie;0))=1))));
     catecuie; MAP(scpecui; LAMBDA(v; LET(cuie; TEXTSPLIT(v;";");
              _find; MAP(cuie; LAMBDA(vv; SUM(--ISNUMBER(FIND(vv; scpecui)))));
               minf; MIN(_find);
               maxf; MAX(_find);
              TEXTJOIN(";";TRUE;minf;_find)
             )));
     minime; TAKE(--TEXTSPLIT(TEXTJOIN("|";;catecuie);";";"|");;1);
     minm; MIN(minime);
     cuief; FILTER(cuiei;minime=minm);
  cuief
)

Multe căutări în toată această formulă.

Cam asta a fost. Descărcați fișierul schimbați valorile, A, B, C cu alte valori și verificați dacă este ok. Nu dați fișierul tâmplarilor. :)

O zi bună!