Pentru acest articol am continuat partea de vectori din articolul trecut și propun o rezolvare a problemei
OddOccurrencesInArray.
În această problemă ni se propune un vector cu un set de numere naturale, unele dintre ele se repetă. Scopul este de a identifica câte din numerele respectivă se repetă de un număr impar de ori.
Nu mai detaliez mica parte de teorie din articolul precedent ci detaliez direct problema și explic soluțiile.
Se dă șirul {9, 3, 9, 3, 9, 7, 9, 1}. În acest șir sunt unice valorile {1, 3, 7, 9}. Dintre acestea, 1 și 7 apar de un număr impar de ori (o singură dată).

Rezolvarea pas cu pas
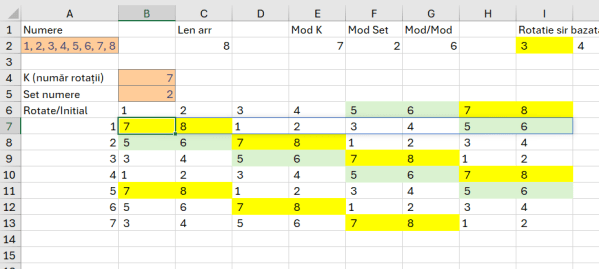
Șirul de numere este trecut în celula A2.
Pentru a descompune șirul în A5 folosesc funcția =–TEXTSPLIT(A2;;”, „) , caracterele – vor transforma rezolvatul text al funcției de split într-un număr.
Pentru a determina valorile unice în C5 folosesc funcția: =SORT(UNIQUE(A5#)) prin care determin valorile unice de pe array A5#, cu funcția UNIQUE() și apoi le sortez în ordine crescătoare cu funcția SORT(). Tendința în Excel este de a transforma cât mai mult operațiile în funcții. Avantajul acestei abordări este că operațiunile nu sunt replicabile, sau pot fi oarecum replicate prin înregistrare și editare de macro. Funcțiile în schimb pot fi replicate și copiate.
Tehnica de apelare cu # este utilă când nu știm câte numere sunt în șir, ceea ce face dinamic rezultatul dar și apelarea sa.
Ca să determin câte valori sunt de fiecare număr folosesc în D5 un simplu COUNTIF() pentru numărarea condiționată a valorilor de pe array A5# cu condiția ca ele să fie egale cu cele din unicele de pe array C5#.
Ca să pot compara dacă valoarea rezultată pe coloana D este un număr impar folosesc funcția ISODD(). Ca să preiau valoarea impară de pe coloana din dreapta folosesc funcția TAKE() cu parametrul -1. Ca să afișez în IF() valoarea de pe coloana din stânga folosesc un TAKE cu valoarea 1. Pentru a scana tot tabelul rezultat din array C5#:D5# linie cu linie folosim funcția BYROW() care are nevoie de un tabel ca input și o funcție LAMBDA() cu parametrul de input r (echivalentul liniei) pentru interpretare.
Pentru a afișa rezultatul final al prelucrării folosesc funcția TEXTJOIN() cu delimitator „, „.
Rezolvarea dintr-o singură funcție
Rezolvarea pas cu pas a fost aproape o nimica toată, cheia fiind BYROW()-ul descris anterior.
Ca să rezolvi problema într-o singură funcție, ai aproape întotdeauna pentru probleme puțin mai complexe de funcția LET() în care poți compune gradual variabilele pe care pot fiu folosite în alte funcții din același LET(). LET()-urile se pot combina între ele cu alte funcții. Doar că una din funcții nu funcționează corect în context de LET(). Minumata funcție COUNTIF() returnează eroare de fiecare dată când încerci să o incluzi în LET().
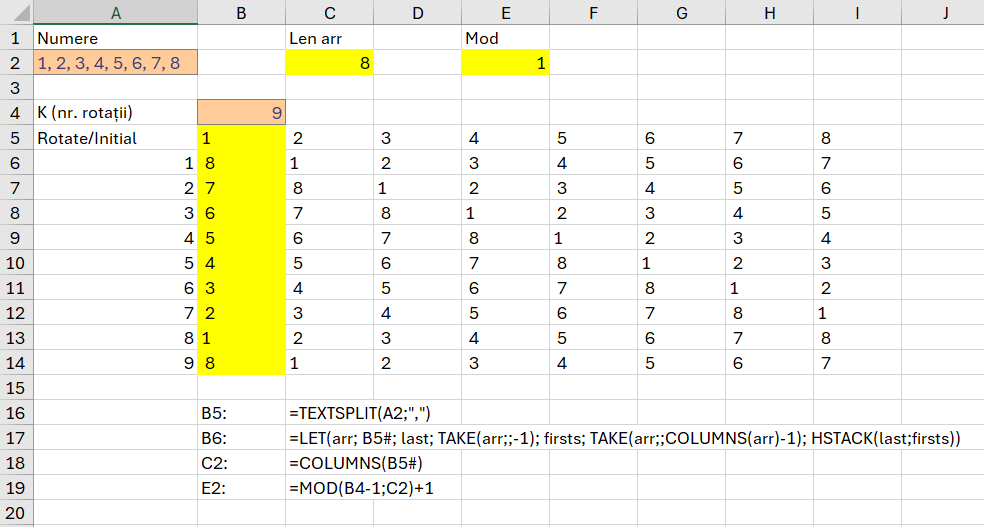
Într-o abordare conform scenariului anterior, funcția intermediară de determinare a fiecărei apariții a numărului ar fi trebuit să arate ca în imagine:

în care funcția MAP() ar trebui să parcurgă element cu element din valorile unice, iar LAMBDA() ar trebui să execute operațiunea de numărare condiționată a vectorului rezultat arr, pentru fiecare valore. Doar că nici COUNTIF() nici COUNTIFS() nu returnează valori corecte în acest context. Am încercat să realizez o funcție personalizată ca să includă COUNTIF()-ul și MAP() nu funcționează.
În acest context a trebuit să schimb funcția și în loc de un COUNTIF() să fac un COUNT() de un FILTER().
Funcția finală:
=LET( arr;--TEXTSPLIT(A2;;", ");
unice; SORT(UNIQUE(arr));
cate; MAP(unice;
LAMBDA(v; COUNT(FILTER(arr; arr=v))));
interm; HSTACK(unice;cate);
TEXTJOIN(", ";TRUE;
BYROW(interm;
LAMBDA(r;IF(ISODD(TAKE(r;;-1));TAKE(r;;1);""))))
)în care aplic tehnicile descrise anterior pentru a obține un șir cu valorile care apar într-un număr impar de ori într-un șir de numere naturale.
Descrierea variabilelor:
- arr – preia șirul și-l descompune apoi îl tranformă în număr;
- unice – sortează valorile unice de pe arr;
- cate – pentru fiecare valoare (v) din unice (MAP), aplică o funcție LAMBDA pentru a număra rezultatul fintrării arr după v curentă. Unice și Cate sunt variabile de o singură coloană care au același număr de rânduri.
- interm – este variabila prin care realizez o matrice din cele două variabile;
- matricea interm este parcursă de BYROW() prin care aplic o funcție LAMBDA() pentru fiecare linie (r) în așa fel încât să determin dacă valoarea de pe coloana din dreapta (TAKE cu -1) este număr impar (funcția ISODD).
Update 24.04.2024
În cazul în care vrem totuși să optimizăm execuția în loc să folosim funcția COUNT() de FILTER() ar fi mai util să folosim SUMPRODUCT() un fel de substitut pentru COUNTIF() și care funcționează atât în LET cât și în MAP().
Pentru a determina numărul de apariții a ficărui număr atunci putem folosi funcția:
=LET( arr;--TEXTSPLIT(A2;;", ");
unice; SORT(UNIQUE(arr));
cate; MAP(unice;
LAMBDA(v; SUMPRODUCT(--(arr=v)))); cate)Cam asta este. Nu sunt sigur că este cea mai optimă variantă. Dacă aveți alte modele de rezolvare inclusiv în alte limbaje (Phyton de exemplu, sau VBA) sau vă rog să le partajați în comentarii dacă doriți.
Sper să fie util cuiva.