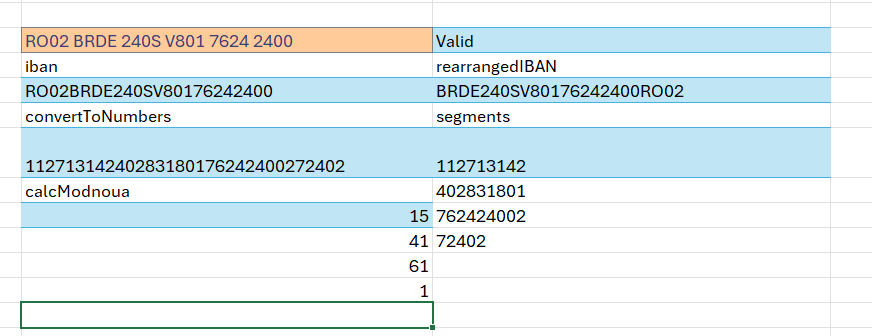
În acest articol voi propune diferite metode de rezolvare a problemelor clasice de algoritmică cu focus pe zona de stive și cozi, probabil cele mai utilizate concepte în programare și mai ales în lucrul cu datele. Cum am mai spus cu diferite ocazii, Excelul nu ar trebui să fie un instrument pentru colectarea, stocarea și gestionarea unui volum mare de date, ci mai mult un instrument de analiză și rafinare rapidă a unor seturi restrânse de date. Da, poate face asta dar uneori nu foarte eficient, sau efortul este mai mare decât dacă ai utiliza alte instrumente.
Problemele supuse rezolvării sunt descrise pe site-ul Codility: https://app.codility.com/programmers/lessons/7-stacks_and_queues/ unde de obicei se propun rezolvări programatice.
O mică delimitare conceptuală
Excelul se dezvoltă rapid datorită numărului mare de utilizatori din variate domenii de activitate, dar și creativității acestora. La ora actuală vorbim despre mai multe metode de rezolvare a diferitelor probleme în Excel dintre care amintim:
- Excel clasic
- utilizarea formulelor și funcțiilor clasice
- utilizarea unor instrumente clasice de rezolvare probleme: Pivot table, Data table, Solver
- utilizarea VBA, tehnologie pe care eu personal o consider depășită
- Excel modern
- utilizarea Power Pivot și Power Query (limbaj m)
- utilizarea DAX
- utilizarea Automate (un înlocuitor modern al VBA, dar încă la început de drum)
- utilizarea Dynamic arrays.
Ceea ce vă propun eu prin seria de articole despre algoritmi este utilizarea Dynamic arrays, parte componentă a Excel modern. Sunt convins că aceste probleme se pot rezolva și cu celelalte metode.
Marele dezavantaj al funcțiilor actuale care lucrează cu dynamic arrays este acela că nu au integrată funcția de prelucrare iterativă for din programare clasică.
Pentru că toți învățăm de la cineva, citez și eu în acest articol, câteva metode de a rezolva diferite probleme de iterații în excel în locul for-ului propuse de Diarmuid Early, vicecampion modial Excel eSports, în videoclipul Write Excel firmulas like a programmer.
Câteva concepte teoretice
Așa cum menționam în Excel nu avem for. Cu ce facem iterațiile atunci? Nu putem face iterații adevărate dar putem simula iterațiile prin utilizarea unor combinații de funcții Sequence combinate cu scan, map, reduce, byrow, bycol.
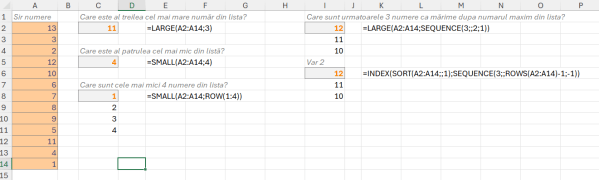
În imagine câteva exemple de utilizare a funcției sequence():
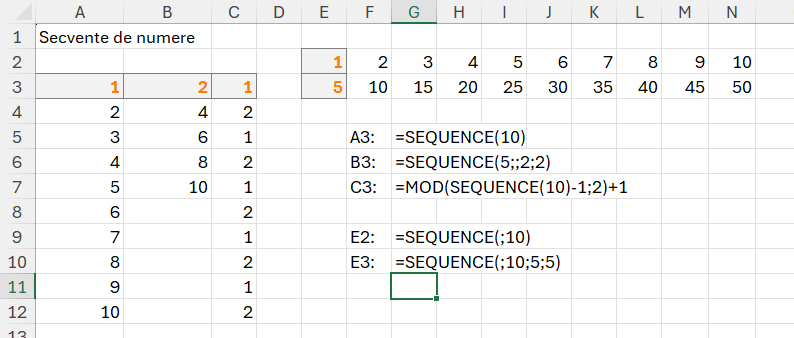
Parametrii lui sequence sunt:
- Rows: numărul de linii pe care dorim să le generăm (exemplu în A3 avem 10 linii)
- Columns: numărul de coloane pe care dorim să le generăm (exemplu în E2 primul parametru rows nu este completat și formula începe direct cu separatorul ; (punct și virgulă) echivalentul , (virgulă) din versiunea în engleză.
- Start: numărul de la care să pornească numerotarea (exemplu în B3, generăm 5 numere pe o coloană (rows) pornind de la valoarea 2. În E3, pornim de la 5)
- Step: pasul de creștere, implicit 1.
În C3 combin un sequence care generează 10 numere cu un mod prin artificiul -1/+1 pentru a putea obține 10 numere în formatul dat.
Cele mai utilizate funcții de scanare a vector sunt prezentate în imagine:

SCAN și REDUCE au aceeași sintaxă, numai că scan calculează pentru fiecare element din vector, adică ajungem pas cu pas la valoarea finală, rezultatul fiind un array de valori, pe când REDUCE calculează direct valoarea finală. Parametrii celor două funcții sunt:
- valoarea inițială de la care pornim, în cazul meu 0 în ambele cazuri (B16 și C16);
- vectorul de scanat, în cazul meu A16#;
- funcția lambda care se ocupă cu modul de calcul efectiv. Cheia în această funcție este că are doi parametri: a și v în această ordine. A este valoarea acumulată prin operațiunile returnată de lambda până la V, valoarea curentă.
Foarte important de știut: SCAN nu lucrează cu tabele de date și nici nu returnează tabele de date ci un singur vector. Dacă dorim să lucrăm totuși cu tabele, atunci putem reduce întreg tabelul la un vectori de valori prin concatenare după care să lucrăm cu artificiul prezentat data trecută de splitare în linii și coloane:
split; IFNA(--TEXTSPLIT(TEXTJOIN("|";1;tabelrezultat);";";"|");"");MAP este o funcție la fel de interesantă, care are doar 2 parametri: vectorul de parcurs și funcția lambda pentru calcule care are ca parametru de intrare valoarea curentă (v). Da, putem face cu un MAP ce facem cu un SCAN, vezi formula din E16, doar că într-un mod oarecum mai complicat. Personal consider că scan este recomandat, dar uneori se complică problemele când dorești să lucrezi cu valoarea anterioară nu cu acumulatorul. Veți vedea mai jos.
Combinând între ele sequence cu scan putem emula operațiuni for în Excel, chiar dacă unele variante cu stop la o anumită condiție, încă nu știu cum să le rezolv. :)
În continuarea articolului voi prezenta câteva propuneri de rezolvare a problemelor de pe Codility.
Problema Brackets
Problema „Brackets” face parte din categoria algoritmilor de tip Stacks and Queues și este folosită pentru a verifica corectitudinea unui șir de paranteze. Aceasta este o problemă clasică de validare a echilibrului și închiderii corecte a parantezelor într-un șir.
Enunțul problemei: Un șir de caractere conține următoarele tipuri de paranteze: (), {}, []. Trebuie să determinăm dacă șirul de paranteze este corect închis și echilibrat. Un șir de paranteze este considerat corect dacă:
- Fiecare paranteză deschisă are o paranteză corespunzătoare închisă de același tip.
- Parantezele închise sunt în ordinea corectă.
Exemplu
(), ([]{}), {[()()]} sunt șiruri corecte.
(], ([)], {{{{ sunt șiruri incorecte.
Modelul este destul de bizar, am încercat diferite abordări, clasic prin descompunerea într-un vector… dar fără succes, iar dacă cumva riscați să încercați o rezolvare cu ChatGPT… treaba e tristă rău. :) Doar încercați…
Propunerea mea de rezolvare după ceva abordări matematizate și care mai de care mai alambicate:
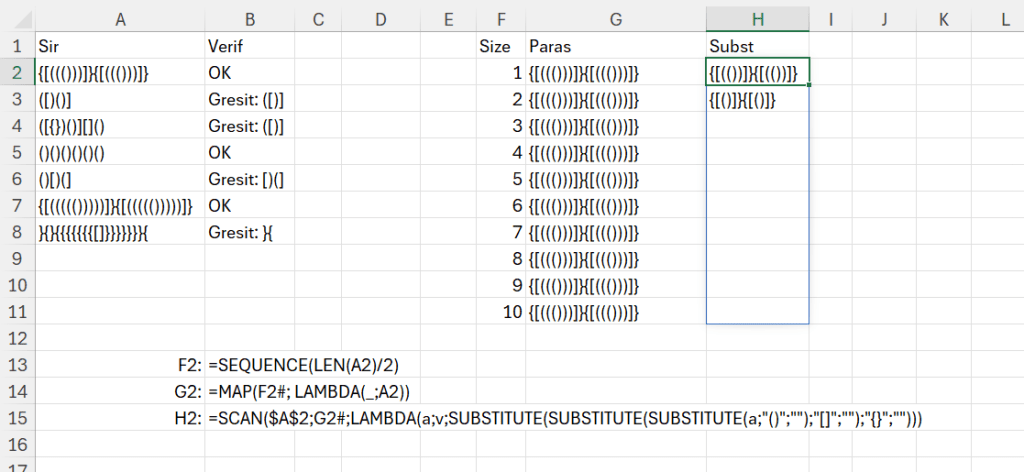
În rezolvarea problemei am pornit de la generarea unei secvențe de jumătate din lungimea totală a șirului de paranteze. Practic ele vin în perechi deschis, închis deci nu ar trebui să existe mai multe rulări. După care pentru a putea scana și substitui perechile deschis închis ca să vedem dacă rămâne una închisă eronat sau neînchisă, am replicat șirul de paranteze de dimensiunea secvenței generate prin maparea șirului de secvență și utilizarea unei fake Lambda, în care parametrul de intrare, în loc de V l-am înlocuit cu _ (undescore) pentru că nu-l folosesc la nimic.
În scanul din H2, care pornește de la șirul inițial din A2 și verifică pe G2 (care este un V identic), am substituit pe rand parantezele din valoarea acumulată. Ceea ce înseamnă că el de fapt face o substituție repetitivă pentru câte rulări i-am specificat prin Size. Rezolvarea nu este optimă din punct de vedere algoritmic pentru că în fiecare pas execut un număr determinat de la început de pași. Așa cum specificam în partea de teorie nu putem să oprim execuția la îndeplinirea unei condiții ci executăm în continuare după un număr de pași prestabiliți.
În formula pentru o singură celulă am vrut să integrez și secvența de paranteze care nu se potrivește.
Funcția integrată:
=LET(sir;A2;
size;SEQUENCE(LEN(sir)/2);
paras;MAP(size;LAMBDA(_;sir));
subst;SCAN(sir;paras;LAMBDA(a;v;SUBSTITUTE(SUBSTITUTE(SUBSTITUTE(a;"()";"");"[]";"");"{}";"")));
lastval;TAKE(subst;-1);
IF(LEN(lastval)=0;"OK";"Gresit: "&lastval))În care în ultima parte am preluat ultima valoare a lui Scan care reprezintă parantezele care nu se potrivesc.
Având în vedere că sunt funcția propusă se aplică la toate tipurile de paranteze, aceeași soluție funcționează și pentru Problema Nesting de pe Codility.
Care este aplicabilitatea acestui tip de problemă?
Un pic forțat, un model de aplicabilitate ar fi acela de evaluare a unei secvențe de cod JSON, pentru a verifica dacă este valid din punct de vedere al parantezelor.
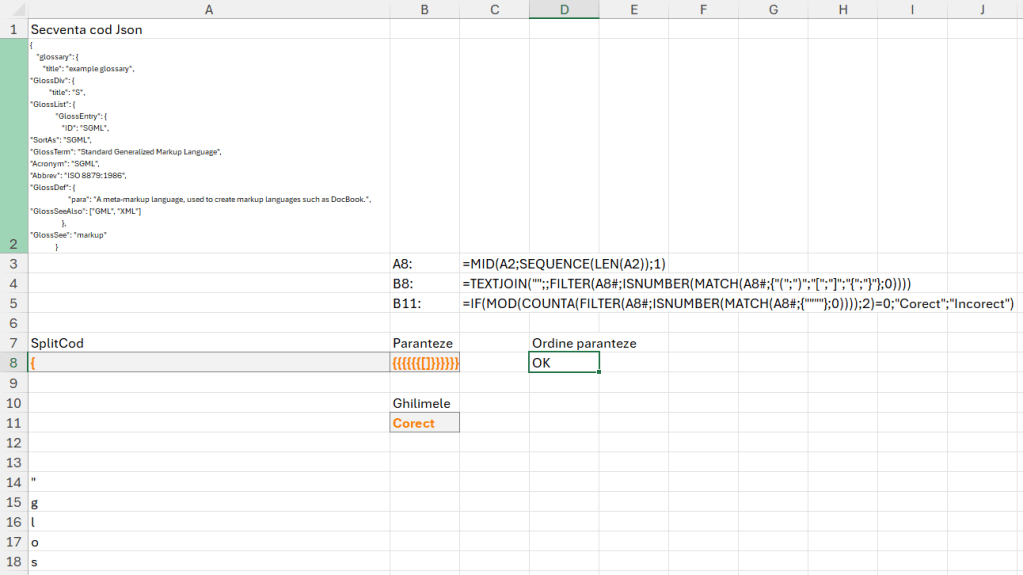
În același exemplu, în B11 am verificat și dacă ghilimelele sunt deschise și închise corect.
De asemenea, cred că putem defini și alte simboluri pe post de închidere / deschidere care ar putea fi verificate.
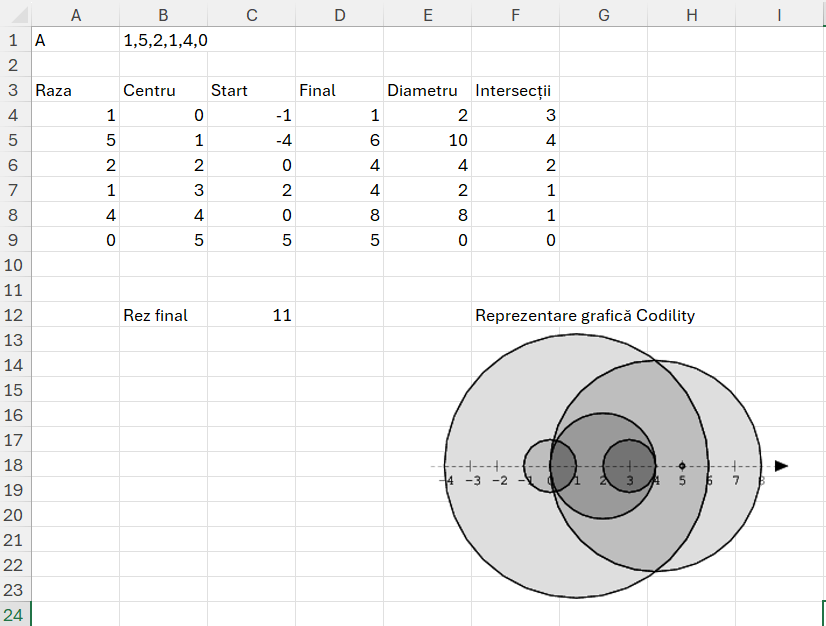
Problema Fish
Problema în care peștele cel mare îl mănăncă pe cel mai mic… mi-a dat cele mai dureroase bătăi de cap până acum. De ce? Pentru că trebuie să parcurgi un tabel cu două coloane de un număr necunoscut de ori.
Descrierea Problemei: Avem un râu în care n pești înoată în direcții opuse. Fiecare pește este descris de două atribute:
- Un număr întreg care reprezintă mărimea peștelui. (A)
- O direcție care poate fi 0 (înoată în amonte) sau 1 (înoată în aval). (B)
Peștii din amonte și aval își urmează cursul până când se întâlnesc. Atunci când doi pești se întâlnesc:
Dacă peștele din amonte (0) este mai mic decât peștele din aval (1), peștele din amonte este mâncat.
Dacă peștele din aval (1) este mai mic decât peștele din amonte (0), peștele din aval este mâncat.
Dacă cei doi pești au aceeași mărime, peștele din aval (1) va mânca peștele din amonte (0).
Scopul problemei este să determinăm câți pești vor supraviețui după ce toți peștii care se pot întâlni și mânca au făcut acest lucru.
Propunere de rezolvare:

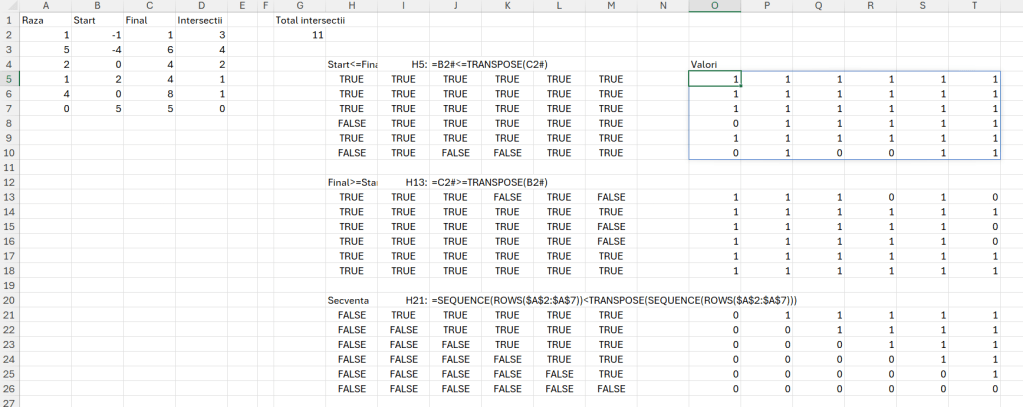
Ca să pot rezolva această problemă mi-am dat seama după mult timp că cea mai bună abordare este cu SCAN și căutări permanente și comparare cu valoarea anterioară sau valoarea următoare în funcție de direcția în care se mișcă peștele. Ca să ajung la funcția din G2, am trecut prin mai multe variante, una intermediară este acea a rulărilor care încep cu coloana K în care input pentru Run 01 este o concatenare a tabelului, iar pentru Run 02 încolo este rezultatul anterior. Aici a fost de fapt cheia: cum folosești un tabel ca un input recursiv?!
Funcția propusă în celula G2:
=LET(ari; A2:B6; seqc; SEQUENCE(;ROWS(ari)*2);
fscani; LAMBDA(arri; LET(arr; arri;
rrs; ROWS(arr); seq; SEQUENCE(ROWS(arr));
fH; LAMBDA(x; TEXTJOIN(";";TRUE;INDEX(arr;x;1);INDEX(arr;x;2)));
fIndexP; LAMBDA(x; LET(ba; INDEX(arr;x-1;2); bc; INDEX(arr;x;2); bv; INDEX(arr;x+1;2);
aa; INDEX(arr;x-1;1); ac; INDEX(arr;x;1); av; INDEX(arr;x+1;1);
IF(bc=0; IF(ba=1; IF(ac<aa; aa&";"&ba; ac&";"&bc); ac&";"&bc);
IF(bv=1; ac&";"&bc; IF(ac<av; av&";"&bv; ac&";"&bc)))));
fIndexL; LAMBDA(x; LET(ba; INDEX(arr;x-1;2); bc; INDEX(arr;x;2);
aa; INDEX(arr;x-1;1); ac; INDEX(arr;x;1);
IF(bc=0; IF(ba=1; IF(ac<aa; aa&";"&ba; ac&";"&bc); ac&";"&bc); ac&";"&bc )));
rez; SCAN(0; seq; LAMBDA(a;v;
IF( AND(v=1; INDEX(arr;v;2)=0);fH(v);
IF(v=rrs; fIndexL(v); fIndexP(v)))));
rez));
rezfin; REDUCE(0; seqc; LAMBDA(a;v; IF(v=1; TEXTJOIN("|";TRUE;fscani(ari)); TEXTJOIN("|";TRUE;fscani(--TEXTSPLIT(a;";";"|"))))));
pestiramasi; UNIQUE(--TEXTSPLIT(rezfin;";";"|"));
nrpestiramasi; ROWS(pestiramasi);
pestiramasi
)Rezultatul final este stocat în variabila rezfin care folosește o funcție REDUCE pe baza seqc variabilă ce definește o secvență pe coloane de numărul de elemente supuse analizei. Aici este problema de optimizare pe care nu am reușit să o rezolv în așa fel încât să determin optimul de rulări. În REDUCE folosesc funcția recursivă fscani cu parametrul de intrare ari dacă suntem la primul element din vector (v=1) sau a, dacă suntem la următoarele valori.
fscani este compus la rândul său din din mai multe funcții:
- fH – utilizată pentru a concatena valorile celor două coloane de pe poziția 1, începutul scanului;
- fIndexP – utilizată pentru a concatena valorile de dinainte sau de după înregistrarea curentă în funcție de 1/0 sau dimensiune, în care prin Index aducem valoarea dimensiunii peștelui: anterioară (aa), curentă (ac) sau următoare (av) și valoarea 0/1 specifică deplasării: ba – direcția de deplasare a peștelui anterior, bc, direcția peștelui curent și bv, valoarea peștelui viitor.
- fIndexL – funcție derivată din fIndexP dar pe care o utilizez doar la ultimul element din vector. Aici ar fi mers o optimizare în fIndexP pentru a verifica cazul de eroare în cazul în care nu există valori viitoare.
Rezultatul final al funcției fscani este stocat în variabila rez care este de fapt un alt scan pe secvența inițială și aplică cele 3 funcții pe intervalul 1…n.
O variantă de implementare puțin diferită a acestui algoritm mi-a fost inspirată de un joc de pe telefoanele mobile, în care peștele mai mare care-l mănâncă pe cel mai mic acumulează punctele acestuia, spre final peștele acumulând majoritatea punctelor puse în joc.
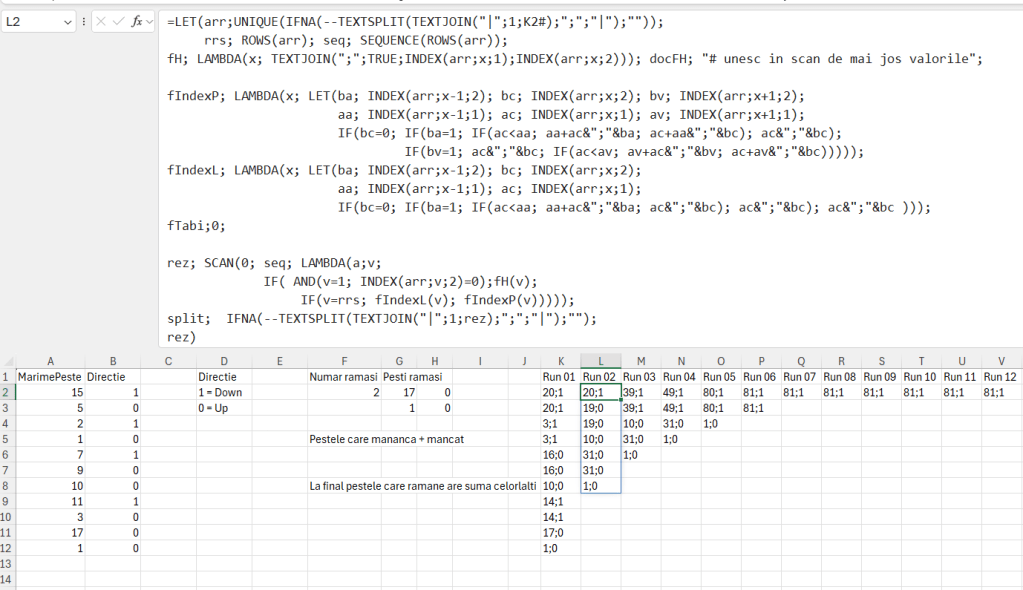
Diferența față de funcția anterioară este că la indexare în momentul în care stabilesc peștele câștigător prin IF-ul din fIndexP în loc să afișez doar valoarea câștigătorului, adun la acesta valoarea celui care a fost mâncat.
Ca aplicabilitate practică a acestui algoritm mă gândesc în general la prioritizarea unor cozi de așteptare și apariția unui eveniment nou sau schimbarea priorității anumitor elemente. Cred că la managementul incidentelor putem utiliza prioritizare pentru a vedea care incident se va rezolva primul sau la portofoliile de investiții sau acțiuni pentru a determina care acțiuni merită vândute și ce trebuie achiziționat pentru maximizarea portofoliului.
Dincolo de toate Fish a fost pentru mine una din cele mai mari provocări tehnice de până acum. Clar, recomand metode programatice dar am demonstrat că se poate și în Excel.
Problema StoneWall
Descrierea problemei: Dându-se o secvență de înălțimi care reprezintă ziduri, trebuie să determinăm numărul minim de blocuri necesare pentru a construi aceste ziduri. Fiecare bloc are aceeași lățime și poate fi plasat în moduri diferite, dar trebuie să acopere întreaga înălțime specificată pentru fiecare zid, iar blocurile pot fi plasate unul peste altul.
Logica rezolvării problemei
Să considerăm șirul de înălțimi H = [8, 8, 5, 7, 9, 8, 7, 4, 8].
8: Adaugă 8 în stivă. (stiva: [8])
8: Este deja 8 în stivă, nu facem nimic. (stiva: [8])
5: 5 este mai mic decât 8, eliminăm 8 din stivă. Adăugăm 5. (stiva: [5])
7: 7 este mai mare decât 5, adăugăm 7. (stiva: [5, 7])
9: 9 este mai mare decât 7, adăugăm 9. (stiva: [5, 7, 9])
8: 8 este mai mic decât 9, eliminăm 9 din stivă. Adăugăm 8. (stiva: [5, 7, 8])
7: 7 este mai mic decât 8, eliminăm 8 din stivă. (stiva: [5, 7])
4: 4 este mai mic decât 7, eliminăm 7 și 5 din stivă. Adăugăm 4. (stiva: [4])
8: 8 este mai mare decât 4, adăugăm 8. (stiva: [4, 8])
Total add-uri: 7
Propunere de rezolvare

În prima parte (formulele afișate) am setat modelul problemei care la bază folosește un filtru dinamic pe poziția curentă (valoarea din B2) din vectorul H. Funcția din F2 este copiată apoi în jos. Vali este de fapt valoarea rezultată anterior, ceea ce ne duce cu gândul la o rezolvare integrată la acumulatorul dintr-un scan.
Valorile Iterm sunt apoi concatenate în J2, iar cu find-ul din K2, determin dacă există (1) adăugiri sau nu (0).
În P2 am stocat varianta finală integrată al cărei cod este:
=LET(arr;A2:A10;seq;SEQUENCE(ROWS(arr));
vals; SCAN(0;seq;
LAMBDA(a;v;
IF(v=1;""&INDEX(arr;v);
IF(ISERROR(XMATCH(INDEX(arr;v);--TEXTSPLIT(a;";");0));
TEXTJOIN(";";TRUE;FILTER(--TEXTSPLIT(a;";"); --TEXTSPLIT(a;";")<=INDEX(arr;v);"");INDEX(arr;v));
TEXTJOIN(";";TRUE;FILTER(--TEXTSPLIT(a;";"); --TEXTSPLIT(a;";")<=INDEX(arr;v);""))))));
ver; SCAN(0; seq; LAMBDA(a;v; IF(v=1;1;IF(ISERROR(FIND(INDEX(vals;v);INDEX(vals; v-1)));1;0))));
SUM(ver))În care ver este variabila de verificare prin scanare a rezultatelor intermediare direct concatenate cu Textjoin din vals.
Ca aplicabilitate practică mă gândesc la diferite probleme de optimizare a utilizării unor elemente în obținerea celui mai bun rezultat.
Cam atât pentru acest articol!
Sper să fie util cuiva!