Acest articol este o continuare a seriei de articole cu propunere de rezolvare a algoritmilor clasici în Microsoft Excel ediția 365. Probelemele de astăzi fac parte din algoritmii Leader descriși la adresa: https://app.codility.com/programmers/lessons/8-leader/
Algoritmul Leader se referă la identificarea unui element dintr-o secvență de valori care apare mai mult de jumătate din numărul total al elementelor din acea secvență. Acest element este denumit „leader” sau „dominator”. Problema se poate formula astfel: având un vector de dimensiune N, să se găsească elementul care apare de cel puțin N/2 + 1 ori, dacă există unul. În mod programatic se recomandă rezolvarea acestor tipuri de probleme cu algoritmul Boyer-Moore majority vote.
Doar că Excelul este puțin diferit și este mai greu de adaptat la rezolvările clasice care implică secvențe FOR. Alternative există și unele din ele sunt foarte interesante. Dar să începem cu:
Un pic de teorie
În mod clasic dacă am avea un șir de numere sau valori ar trebui să identificăm unicele, apoi să facem un countif pe blocul inițial.

De exemplu în E3: folosim funcția UNIQUE() pentru a calcula elementele unice din vectorul A2:A7, după care utilizăm un COUNTIF() dinamic pe vector după rezultatul din E3#. În felul acesta determinăm numărul de apariții a fiecărui element. Există și o variantă puțin diferită, de a folosi funcția FREQUENCY() în forma: =FREQUENCY(A2:A7; UNIQUE(A2:A7)) dar ea determină doar numărul de apariții a fiecărui element, în cazul nostru 3/3.
În Excel în schimb există o altă funcție MODE cu două variante: SNGL sau MULT. MODE.SNGL() extrage dintr-un șir de valori cea prima cea mai frecventă valoare. În exemplu nostru (B3) avem două valori care au același număr de apariții, ceea ce înseamnă că va afișa doar prima valoare întâlnită în vectorul de căutare. MODE.MULT() extrage cele mai frecvente numere, în cazul în care avem egalitate la numărul de apariții le va afișa pe ambele. În cazul în care nu avem nici un leader, funcția MODE va afișa eroarea #N/A.
O abordare interesantă este în schimb la text, pentru că MODE.MULT() funcționează doar la valori numerice. În modelul propus în imaginea anterioară, ca să putem determina leaderul folosim un MODE dar pentru un MATCH care extrage pentru fiecare valoare întâlnită poziția inițială a sa. După care pe același șir extragem valoare pentru cea mai mare valoare. MODE() în formatul clasic încă este funcțional și compatibil în Excel 365.
Problema Dominator
În problema Dominator ni se cere să determinăm care este numărul dintr-un vector care apare de mai mult de jumătate din lungimea vectorului. De asemenea, se poate solicita extragerea pozițiilor din vector în cazul în care avem un număr Dominator.
Propunerea de rezvare pas cu pas:
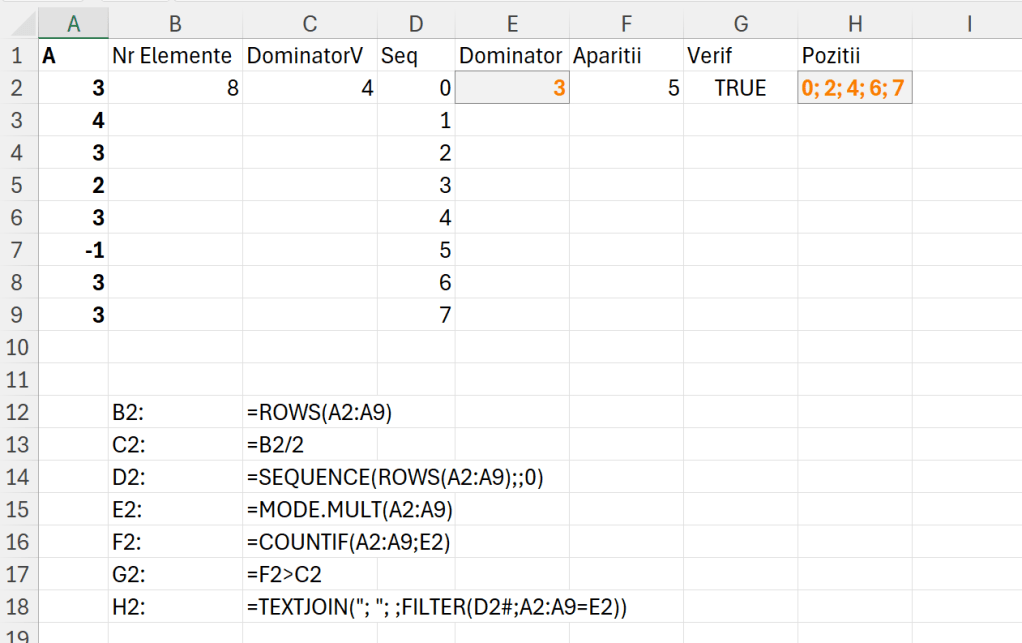
Ca să determin Leader-ul este simplu să folosim un MODE.MULT() în E3, dar ca să determinăm dacă este dominiator avem nevoie de numărul de elemente din vector (B2), valoarea de dominare care este numărul de elemente împărțit la 2 (C2), numărul de apariții (F2), verificarea că Leaderul este dominator (G2), iar dacă dorim să extragem pozițiile în vector va trebui să folosim o secvență cu start de la 0 (D2) pe care să o filtrăm după pentru cazurile în care A este egal cu Leader care devine dominator.
Unificat într-o singură funcție cu LET() aceasta ar fi:
=LET(arr; A2:A9;
nrEl; ROWS(arr);
dominatorv; nrEl/2;
seq; SEQUENCE(nrEl;;0);
dominator; MODE.MULT(arr);
verifi; ROWS(dominator)=1;
aparitii; COUNTIF(arr; dominator);
verifii; aparitii>dominatorv;
IF(AND(verifi; verifii);
TEXTJOIN("; "; ; FILTER(seq; arr=dominator));
"Nu există dominator"))În funcție am două verificări: verifi și verifii. În verifi verific dacă am un singur rezultat sau mai multe. În cazul în care sunt returnate mai multe valori prin MODE.MULT atunci nu avem un dominator ci mai mulți Leaderi. În rest logica funcției este descrisă în secțiunea de rezolvare pas cu pas.
Problema EquiLeader
Aceasta este o versiune mai complexă a problemei Dominator pentru că presupune compararea dinamică a leaderilor pe două secțiuni ale aceluiași vector. În această problemă, trebuie să determinăm numărul de poziții dintr-un array unde liderii celor două sub-secvențe (stânga/sus și dreapta/jos) sunt identici. Concret: Având un array A de dimensiune N, o poziție S este un echileader dacă liderul sub-secvenței A[0…S] este același cu liderul sub-secvenței A[S+1…N-1]. Trebuie să găsim numărul total de astfel de poziții în array.
După citirea enunțului am realizat că logica de rezolvare este identică cu problema TapeEquilibrium din articolul Modele de algoritmi in #Excel – Time complexity (3) .
Propunere rezolvare în Excel:
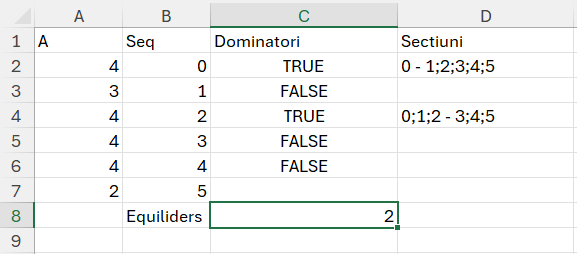
În care pe coloana C determinăm dacă în poziția curentă comparată cu celelaltă secțiune avem egalitate de Dominatori, iar pe coloana D afișăm combinațiile de pe secvența de pe B. Funcția de pe C și D este aceeași cu specificarea că rezultatul final este afișat diferit.
=LET(arr;A2:A7;poz;SEQUENCE(ROWS(arr);;1);
freq; LAMBDA(a; LET(x; a; cate; ROWS(x); unice; UNIQUE(x); dominatorv; cate/2; nrfiecare; COUNTIF(x; unice); tabi; SORT(HSTACK(unice; nrfiecare);2;-1); dominatorval; TAKE(tabi;1;-1); veri; dominatorval>dominatorv; dominator; IF(veri; TAKE(tabi;1;1); 0); dominator));
pp;MAP(poz;LAMBDA(v; LET(ari; INDEX(arr;1):INDEX(arr;v); freq(ari))));
ppa; LET(pozi; B2#; ppa; MAP(pozi;LAMBDA(v; TEXTJOIN(";";;INDEX(pozi;1):INDEX(pozi;v+1)))); ppa);
dp;MAP(poz;LAMBDA(v; LET(arii; (INDEX(arr;v+1):INDEX(arr;ROWS(arr))); freq(arii))));
dpa;LET(pozi; B2#; ppa; MAP(pozi;LAMBDA(v; TEXTJOIN(";";;INDEX(pozi;v+2):INDEX(pozi;ROWS(arr))))); ppa);
domins;IFERROR(pp=dp; "");
nrequi; SUM(IFERROR(--domins; 0));
care; IFERROR(IF(domins; ppa&" - "&dpa;"");"");
domins
)Cheia în rezolvarea problemei, este funcția freq care este utilizată recursiv în MAP-ul care calculeaza valoarea pp și dp. freq este de fapt funcția de determinare a dominatorului din problema Dominator, dar care este generalizată pentru a prelua parametrul de intrare a, care se transformă în x în LET() și calculează dominatorul pe subvectorul determinat în pp și dp de index-ul dinamic.
ppa și dpa se folosesc pentru a extrage valoarea din secvență pentru a afișa pozițiile din vector și secțiunile unde întâlnim dominatori egali.
Rezultatul 2 al funcției este numărul de segmente de pe vector care înreplinesc condiția de egalitate între dominatori.
Ca aplicabilitate practică putem să ne gândim la analize de piață pentru a identifica dacă pe diferite segmente sau intervale de timp există un brand dominant.
Cam atât pentru astăzi!
Sper să vă fie util!
