În acest articol propun o metodă de rezolvare a algoritmilor clasici în formatul Excel modern, din categoria Maximul slice. Descrierea acestor probleme o găsiți la adresa: https://app.codility.com/programmers/lessons/9-maximum_slice_problem/
Puțină teorie
Pentru rezolvarea problemelor din acest articol am ales să folosesc cu precădere funcția MAKEARRAY() care poate avea o putere nebănuită de a transforma un vector liniar într-o matrice dacă reușești o proiecție corectă. Sintaxa funcției:
=MAKEARRAY(rows; columns; function) în care rows este numărul de linii care se vor genera cu începere de la R1 , columns la numărul de coloane din tabelul rezultat iar function este o funcție lambda() cu doi parametri: rows; columns.
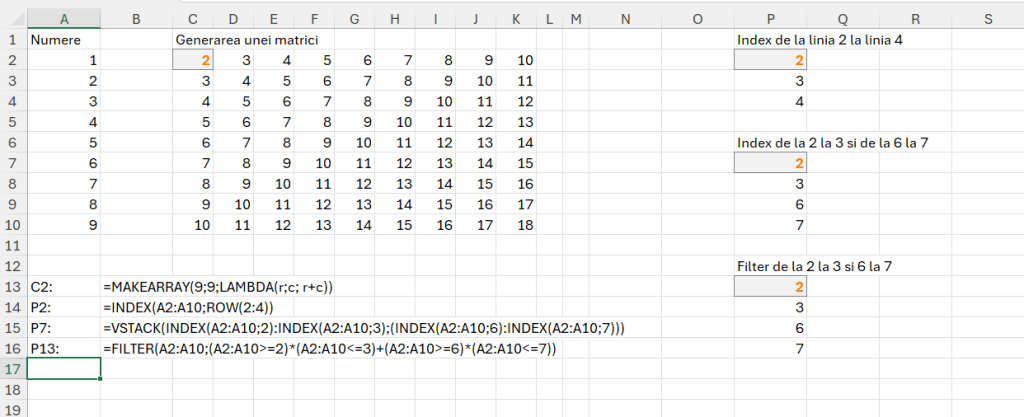
După cum se observă în C2 este generată o matrice cu 9 linii și nouă coloane, pentru fiecare celulă realizându-se calculul r+c, însemnând valoarea rândului cu valoarea coloanei.
Celelalte funcții le-ați mai întâlnit. Mai multe detalii despre Filter puteți găsi în articolul de demult: Funcția Filter() din #Excel 365. Funcția Index() mi-a dat ceva de furcă la problema a treia… dar să ajungem acolo.
Să nu uităm că în algoritmică elementele unui vector încep de la 0, dar în Excel majoritatea operațiunilor de indexare/filtrare/cautare încep de la valoarea 1.
Problema MaxProfit
Face parte din categoria problemelor care analizează secvențe și se concentrează pe identificarea profitului maxim care poate fi obținut printr-o singură tranzacție de cumpărare și vânzare a acțiunilor.
Descrierea problemei: Ni se dă un vector A care conține prețurile acțiunilor în diferite zile. Trebuie să găsim profitul maxim care poate fi obținut cumpărând acțiunile într-o zi și vânzându-le într-o altă zi ulterioară. Dacă nu este posibil să obținem un profit (de exemplu, prețurile scad sau rămân constante), profitul ar trebui să fie considerat 0.
Propunerea de rezolvare:
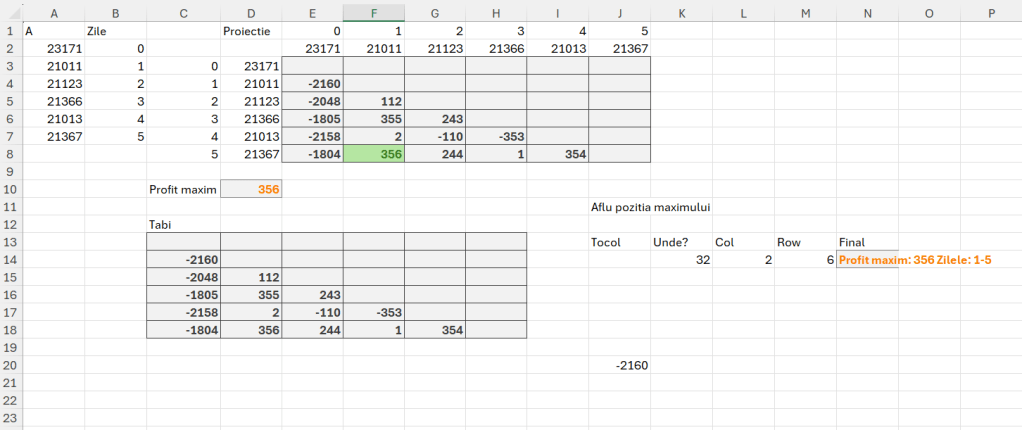
În zona de Proiecție am realizat o implementarea manuală pentru a verifica suma maximă. La urma urmei multe probleme le rezolvăm manual până să ne mai chinuim să facem tot felul de funcții, nu? :) După ce am pus zilele și valoarile pe coloană și linie, la E3 am scris formula: =IF($C3<=E$1;””;$D3-E$2) , întotdeauna zilele trebuie să fie mai mici decât cele pentru care ne raportăm (axa timpului).
Apoi în C13 am proiectat o funcție integrată pentru a face din prima același tabel dar de data aceasta raportându-mă la vectori intermediari prin intermediul valorii lui r și c din makearray. Astfel funcția din C13 este:
=LET(arr; A2:A7;
seq; SEQUENCE(ROWS(arr));
tarr; TRANSPOSE(arr);
tabi; MAKEARRAY(MAX(seq); MAX(seq); LAMBDA(r;c;
IF(r<=c;""; INDEX(arr;r)-INDEX(tarr;c)))); tabi)în care arr stochează vectorul cu sumele de interpretat, seq generează numărul de zile, tarr transpozează numărul de zile pe coloane ca să le pot folosi ca artificiu în tabi care este de fapt un tabel care indexează valorile din arr pe baza liniei și coloanei curente.
Ulterior în D10 facem un max din acel tabel și avem rezultatul final. Ca să obținem și zilele în care avem acele valori în cazul nostru 1 și 5, atunci trebuie să apelăm șa tehnica de identificare a unei valori într-un tabel, descrisă în articolul: Modele de algoritmi in #Excel – Prefix Sums (5.1)
Problema MaxProfit este o problemă clasică de optimizare cu aplicabilitate în diferite contexte financiare în vederea rezolvării problemelor de maximizare a câștigurilor într-o serie de tranzacții.
Problema MaxSliceSum
MaxSliceSum este o problemă clasică în informatică, care face parte din categoria problemelor de optimizare pe secvențe, adică Maximum Subarray Problem.
Descrierea Problemei: Se dă un vector A de numere întregi (pozitive, negative sau zero). Trebuie identificată suma maximă a unui „slice” (subsecvență continuă) din acest vector. Un slice este definit de două indici P și Q din vectorul A, unde P ≤ Q, și include toate elementele de la A[P] până la A[Q].
Este posibil ca toate numerele să fie negative într-un vector, caz în care slice-ul cu suma maximă va fi cel mai mic număr negativ.
La o primă lectură a problemei am crezut ca este asemanator cu: Problema MinAvgTwoSlice, doar că de data aceasta nu mai luăm perechi de câte două elemente ci pot fi toate elementele… dintr-un șir sau doar o secvență P-Q.
Uneori problemele simple ne dau cele mai multe bătăi de cap, așa că a trebuit să mă documentez mai bine, și așa am aflat că de fapt această problemă mai este cunoscută și ca problema subșir de sumă maximă sau Algoritmul lui Kadane, unul foarte cunoscut în lumea programatorilor. Mi-au plăcut foarte mult explicațiile din filmulețul: Algoritmul lui Kadane – Determinarea unui subsir de suma maxima in C++
Să revenim la Excel. După multe încercări și teste am ajuns din nou la funcția Makearray care are o putere nebănuită în bi-dimensional prin parametrii săi r și c din LAMBDA asociat.
În final implementarea algoritmului este ceva spectaculos de simplu și puternic:

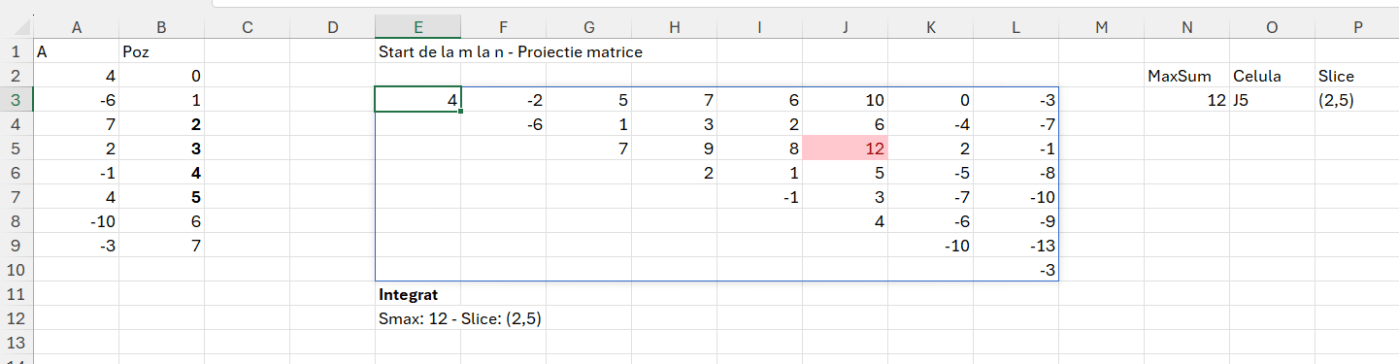
În zona de proiecție matrice am creat un array în care pentru fiecare r<=c am făcut suma subvectorilor de la linia curentă până la coloana curentă.
Funcția din E3 este:
=MAKEARRAY(8;8; LAMBDA(r;c; IF(r<=c; SUM(INDEX($A$2:$A$9;r):INDEX($A$2:$A$9;c));””)))
în care pentru fiecare celulă din tabelul 8 pe 8 calculăm suma valorilor indexului dinamic de la r la c. Comparați cu complexitatea din filmulețul cu implementarea în C++ și poate dați o șansă Excelului. :) Dincolo de glumă pe mine m-a încântat mult soluția, dar vom vedea la următoarea problemă că lucrurile nu sunt chiar atât de roz în Excel….
Funcția integrată care extrage și slice-ul cu sumă maximă este:
=LET(arr; A2:A9;
seq; SEQUENCE(ROWS(arr));
rr; ROWS(arr);
fSlice; LAMBDA(x; LET(aria;x;
ca; MIN(COLUMN(aria))-1;
ra; MIN(ROW(aria))-1;
tc; TOCOL(aria;1);
unde; MATCH(MAX(aria);tc;0);
col; LET(cs; COLUMNS(aria);
c; MOD(unde;cs);
IF(c=0; cs; c));
row; ROUNDUP(unde/COLUMNS(aria);0);
"("&row-1&","&col-1&")"));
sarr; MAKEARRAY(rr; rr; LAMBDA(r;c;
IF(r<=c; SUM(INDEX(arr;r):INDEX(arr;c));"")));
"Smax: "&MAX(sarr)&" - Slice: "&fSlice(sarr))Toată construcția pare mai complicată pentru că am integrat în fSlice tehnica de identificare a locației unei coloane, în vederea afișării slice-ului maxim. Dar toată cheia soluției este în variabila sarr în care am acel MAKEARRAY descris anterior, doar că de data aceasta dinamic pe baza variabilelor definite la început.
Din păcate pentru multe numere în A, Excelul începe să gâfâie. La 1024 de numere algormitmul merge foarte bine dar la 4096 a început deja să dea semne de blocare. Pentru testare am utilizat funcția de generare array aleatoriu: =RANDARRAY(128;1;-50; 200;TRUE) în care se generează 128 de numere întrgi (TRUE) de la minim -50 până la maximum 200. Limita de numere din A este limita numărului de coloane din Excel (16384) pentru a putea opera matricea de calcule.
MaxSliceSum este util în analizarea datelor financiare (de exemplu, determinarea perioadei în care profitul a fost maxim) sau în analizarea performanței sistemelor (de exemplu, identificarea perioadelor de maximă încărcare sau activitate). Această problemă este importantă pentru înțelegerea optimizărilor pe secvențe și este un exemplu clasic de aplicare a algoritmilor de programare dinamică.
Problema MaxDoubleSliceSum
Problema MaxDoubleSliceSum este o extindere a problemei MaxSliceSum, fiind parte din categoria problemelor de optimizare pe secvențe. Scopul este să găsești suma maximă posibilă a unei subsecvențe formate din trei părți neconsecutive dintr-un vector.
Descrierea Problemei:
Se dă un vector A de numere întregi de lungime N (unde N ≥ 3). Trebuie calculată suma maximă posibilă a unui double slice (subsecvență non-consecutivă) definită de trei indici X, Y, și Z (unde 0 ≤ X < Y < Z < N).
Double slice-ul este definit astfel:
– X este începutul primei secțiuni care este exclusă.
– Y este începutul secțiunii incluse în sumă.
– Z este sfârșitul secțiunii incluse, care este exclusă din sumă.
Suma double slice-ului este calculată ca suma tuturor elementelor din A[X+1] până în A[Y-1] și din A[Y+1] până în A[Z-1].
Rezolvarea algoritmului a fost o mare provocare pentru că indexarea nu funcționează absolut deloc într-un context prea dinamic, de aceea a trebuit să găsesc o altă metodă de rezolvare.

În rezolvarea problemei am pornit de la metoda propusă în Problema MaxProductOfThree doar că de data aceasta nu mă mai refer unitar la poziția lui X, Y sau Z ci trebuie să caut în șirul A valorile echivalente din matrice și să le însumez. În rezolvarea pas cu pas am generat întâi matricea XYZ cu toate combinațiile posibile în care X<Y<Z. Apoi pe bază de indexare în I4 am calculat suma elementelor. Funcția utilizată linie cu line:
=LET(arr;$A$2:$A$9;
rr; E4:G4;
x; --TAKE(rr;;1);
y; --CHOOSECOLS(rr;2);
z; --CHOOSECOLS(rr;3);
SUM(IF(x+1=y;0;
INDEX(arr;x+1):INDEX(arr;y-1));
IF(y+1=z;0;
INDEX(arr;y+1):INDEX(arr;z-1))))variabilele x, y și z sunt preluate pentru fiecare linie apoi fac suma prin indexarea de la X+1 la Y-1 și de la Y+1 la Z-1. Merge destul de bine dar nu am reușit să le integrez în aceeași funcție pentru că modelul este prea elaborat pentru a putea să funcțineze funcția INDEX():INDEX().
Ca să pot identifica și studia care sunt valorile care compun rezultatul am creat coloana intermediară K în care am unificat prin aceeași tehnică de indexare dinamică a vectorului A, pe baza valorilor din matrice.
Unificarea într-o singură formulă a fost un coșmar, insistând pe INDEX():INDEX() și câteva zeci de variante de funcții recursive. Până la urmă am realizat că FILTER() cu criterii multiple este mai fezabil pentru că returrnează blocuri de celule însumabile.
Funcția finală din N5 este:
=LET(arr; A2:A9;
seq; SEQUENCE(ROWS(arr));
matrix; LET(vector; arr;
nr; ROWS(vector);
matrix; MAKEARRAY(nr^3; 3;
LAMBDA(i;j;
IF(j = 1;
INT((i-1)/nr^2)+1;
IF(j = 2; MOD(INT((i-1)/nr); nr)+1;
MOD(i-1; nr)+1))));
fReq; LAMBDA(x; AND(INDEX(x;1)<INDEX(x;2);INDEX(x;2)<INDEX(x;3)));
verif; BYROW(matrix; LAMBDA(r; fReq(r )));
tabi; HSTACK(matrix; verif);
unics; FILTER(tabi; (TAKE(tabi;;-1)=TRUE)*(CHOOSECOLS(tabi;3)<nr));
unicsm; CHOOSECOLS(unics;1;2;3);
unicsm);
tabf; HSTACK(arr;seq);
slice; BYROW(matrix; LAMBDA(r; TEXTJOIN(";";;r-1)));
fcautxy; LAMBDA(a;b;
SUM(TAKE(IFERROR(FILTER(tabf;
(TAKE(tabf;;-1)>=a+1)*(TAKE(tabf;;-1)<=b-1));0);;1)));
fcautxyz; LAMBDA(x;y;z; fcautxy(x;y)+fcautxy(y;z));
summax; BYROW(matrix;
LAMBDA(r; LET(x; TAKE(r;;1);
y; TAKE(TAKE(r;;2);;-1);
z; TAKE(r;;-1);
fcautxyz(x;y;z))));
maxsum; MAX(summax);
tabfin; HSTACK(slice; summax);
FILTER(tabfin; TAKE(tabfin;;-1)=maxsum))în care:
- variabila matrix este definită în articolul Problema MaxProductOfThree și este utilizat doar pentru a putea genera matricea de căutare cu X<Y<Z toate combinațiile posibile.
- tabf este de fapt tabelul cu coloana A și secvența de numere în format de start de la 1 pentru a putea să realizez indexarea pe această coloana.
- slice este utilizată pentru a putea genera perechile de x;y;z în formatul array cu start de la 0 rezultatul fiind afișat ulterior în tabfin.
- fcautxy este o funcție recursivă pe care o folosesc mai jos în fcautxyz pentru ca putea extrage cu filter valorile din A, stocate pe prima coloana a lui tabf pe care o preiau cu TAKE(). Simbolul * este folosit pentru condiții cumulative în filter(). Sintaxa pe cumulative este Filter(valori; (Cond1)*(Cond2) ). Filter() a fost soluția salvatoare.
- fcautxyz este funcția recursivă care face suma prin filtrare, definită în fcautxy dar cu aplicare pe Xy și yz. Aici este artificiul suprem prin care am putut folosi o recursivă în atltă recursivă pentru a adresa din două poziții diferite vectorul A.
- summax este un vector de valori intermediare care preia linie cu linie (BYROW) din matrix valorile lui X, Y, Z după care invocă recursiva fcautxyz pentru a calcula suma.
- maxsum calculează valoarea maximă obținută pe summax
- tabfin este tabelul final în care unesc valoarea maximă cu slice după care în rezultatul afișat introduc un nou FILTER de data aceasta pe tabel, în care valoarea obținută să fie egală cu maximum obținut în maxsum.
Huh… a luat ceva timp… dar merită efortul… cu toate că la testare am avut neplăcuta surpriză să constat că numărul maxim de numere din A este de 101… de ce? pentru că rădăcina cubică a numărului maxim de linii din excel (1.048.576) este aproape 101,5…
Aici ajungem la prima limitare a Excelului în rezolvarea acestui tip de probleme. Voi reveni cu o imbunătățire a matricei de triplete care funcționează până la 185 de linii. Veți vedea de ce.
Ca aplicații practice pentru această problemă mă gândesc acum la finanțe, identificarea intervalelor de creștere și scădere a valorii acțiunilor, pentru a găsi cele mai profitabile perioade de vânzare și cumpărare.
sau analiza datelor pentru găsirea secvențelor de date cu cea mai mare variabilitate pozitivă, utile în detectarea anomaliilor sau în analiza trendurilor.
Cam atât pentru astăzi.
Sper să fie util cuiva!