Modele de algoritmi în #Excel – Greedy algorithms (16)

În acest articol propun un model de rezolvare a probelemelor de pe site-ul Codility: https://app.codility.com/programmers/lessons/16-greedy_algorithms/

Un algoritm greedy este o strategie de rezolvare a problemelor care face alegeri pas cu pas, selectând în fiecare moment opțiunea cea mai bună disponibilă, fără a lua în considerare deciziile viitoare.

Principiul de bază este: „Alege ceea ce pare a fi cea mai bună opțiune la fiecare pas, sperând că această strategie va duce la soluția optimă.”

Acești algoritmi sunt simpli și eficienți, dar nu garantează întotdeauna cea mai bună soluție globală.

În Excel nu avem posibilitatea de a face alegeri numaidecât locale, ci problemele trebuie trate la nivel global. Da o strrategie eficientă este să rezolvi pas cu pas problema, din aproape în aproape pentru a putea ajunge la o soluție integrată. Chiar și în rezolvările individuale trebuie să avem în vedere funcții reutilizabile și tratarea globală a vectorilor de input. De aceea în toată această tehnică este esențială funcția MAP() pentru parcurgerea element cu element a unui vector sau SCAN() tot pentru parcurgere globală, dar cu avantajul acumulării.

Un pic de teorie aplicată

În această secțiune doar voi reaminti cum funcționează o funcție MAP(), SCAN() și BYROW().

Foarte important: Nici una din funcții NU generează tabele. De aceea, în exemplele mele vedeți foarte mult TEXTJOIN() și TEXTSPLIT() ca să pot acumula rezultatele intermediare într-o singură valoare. Dar ca să le pot prelucra trebuie să le splitez ca numere.

MAP() este o funcție care parcurge un vector valoare cu valoare de sus în jos. În multe cazuri putem folosi MAP() pentru a scana un fake vector, generat de exemplu de o funcție SEQUENCE pentru a putea face căutare și înainte pe un vector de valori. De cele mai multe ori dacă dorim să obținem printr-o singură formulă un tabel trebuie să le încapsulăm într-un LET(). Nu am exemple în acest moment despre combinații între MAP() și SCAN(). De obicei eu personal aleg să le tratez separat sau să se separ în funcții recursive distincte.

Sintaxa generică este: =MAP(vector; LAMBDA(valoare; calcule))

Pentru D10 formula este:

=MAP(B10#;  LAMBDA(v; IF(v=1;INDEX(A10:A14;v); INDEX(A10:A14;v)+INDEX(A10:A14;v-1))))

Pentru E12 unde este o variantă cu mai puține inputs (doar variabila _a este input), formula este:

=LET(_a;A10:A14;
    seq;SEQUENCE(ROWS(_a));
    MAP(seq;LAMBDA(v; IF(v=1; 
                           INDEX(_a;v); 
                           INDEX(_a;v)+INDEX(_a;v-1)
 ))))

Tehnica aceasta de a folosi o secvență este des întâlnită în rezolvarea acestor probleme și nu numai.

Func’ia SCAN() este foarte utilă pentru prelucrări cu acumulare.

Sintaxa generică este: =SCAN(valoare_inițială; vector; LAMBDA(acumulator; valoare; calcule))

REPT() este o funcție de replicare a unui șir de un număr specificat de ori.

BYROW() este o funcție care tratează un tabel de date linie cu linie. Similar cu BYROW este BYCOL(). Când dorim să facem calcule simple, atunci putem specifica direct funcția după specificarea tabelului. Dacă avem veva mai mult de calcul, sintaxa generală este: =BYROW(tabel; LAMBDA(linie; calcule))

Funcția TAKE(), CHOOSECOL() sau INDEX() au un rol important în tratarea element cu element a unei linii.

Acestea fiind spuse o să încep atipic această rezolvare cu a doua problemă… pentru că este mai simplă.

Problema TieRopes

Presupune să se determine numărul de funii de o anumită lungime K specificată care pot fi create prin însumarea (înodarea) capetelor dintr-un șir de valori date (A). Valoarea capetelor nu poate depăși K dar funiile pot avea dimensiuni mai mari sau egale cu K. Ordinea de însumare este consecutivă nu se acceptă ca un segment A[0] să fie legat de un alt segment A[n].

Rezolvarea problemei în Excel este foarte simplă, dar rezultatele obținute prin rezolvare locală (subșiruri continue fără verificare globală înainte și înapoi) pot fi oarecum discutabile.

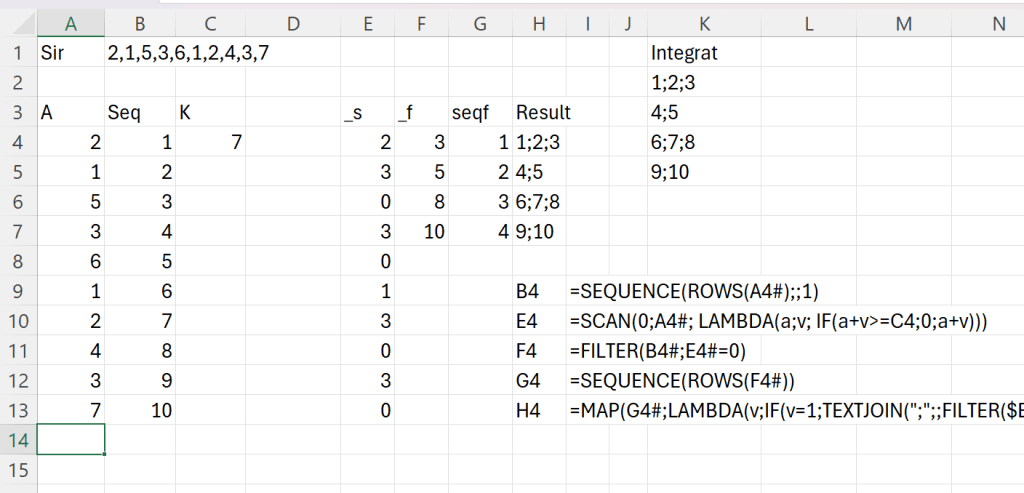
Pornind de la șirul din B2, l-am descompus în A4 apoi am calculat secvența cu start de la 1 în B4. Cheia problemei este în E4 unde prin SCAN am comparat sumele acumulate până în prezent din vectorul A cu valoarea lui K (dimensiunea minimă a unei funii). Ca să pot oferi rezultatele în format de segmente, în H4 am utilizat următoarea formulă:

=MAP(G4#;LAMBDA(v; IF(v=1;
       TEXTJOIN(";";;FILTER($B$4#;($B$4#<=INDEX(F4#;v))));
       TEXTJOIN(";";;FILTER($B$4#;($B$4#<=INDEX(F4#;v))*(($B$4#>INDEX(F4#;v-1))))))))

În care scanez vectorul din G3 rezultat în urma prelucrărilor și pe baza valorii acestui vector concatenez cu TEXTJOIN() valorile de până în acel moment.

Formula integrată pornind de la șirul din B2 și valoarea lui K din C4 este:

=LET(_a; --TEXTSPLIT(B1;;",");
      seq; SEQUENCE(ROWS(_a)); _k; C4;
      _s; SCAN(0;_a; LAMBDA(a;v; IF(a+v>=_k;0;a+v)));
      _f; FILTER(seq; _s=0);
      seqf; SEQUENCE(ROWS(_f));
      result; MAP(seqf; LAMBDA(v; IF(v=1; 
             TEXTJOIN(";";;FILTER(seq;(seq<=INDEX(_f;v))));
             TEXTJOIN(";";;FILTER(seq;(seq<=INDEX(_f;v))*
                     ((seq>INDEX(_f;v-1))))))));
result)

Exemplificare practică

Presupunem că avem un lanț de aprovizionare logistic pentru un retailer care trebuie să transporte pachete mici de produse între depozite și punctele de vânzare. Aceste pachete au greutăți variabile, iar pentru a reduce costurile de transport, ele trebuie grupate în unități mai mari, dar respectând anumite restricții minime de greutate pentru eficiență.

Sintetizând descrierea trebuie să respectăm condițiile:

• Fiecare palet să aibă o greutate minimă K pentru ca transportul să fie eficient (sub această valoare, paletul nu este rentabil).
• Trebuie să formăm cât mai mulți paleți, pentru a maximiza utilizarea spațiului din camion și a reduce numărul de transporturi.

Exemplu concret de date:
Să presupunem că avem un set de 10 pachete cu următoarele greutăți (în kg): A=[3,5,1,6,2,4,8,3,7,2] și greutatea minimă necesară pentru transport eficient este K=10 kg.

Rezolvarea este foarte simplă:

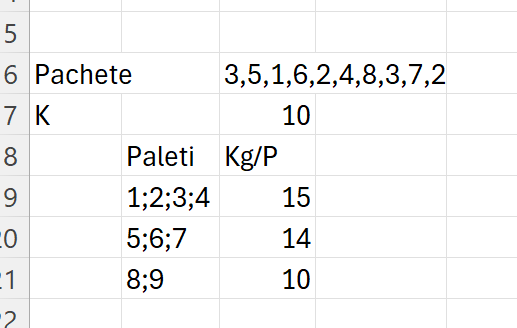
în care pentru a calcula numărul de kg pe fiecare palet am introdus o nouă variabilă în funcția prezentată anterior:

kgp; MAP(result; LAMBDA(v; SUM(INDEX(_a;--TEXTSPLIT(v;;";")))));

care presupune însumarea valorilor coletelor din șirul dat.

Problema MaxNonoverlappingSegments

Problema aceasta a fost un coșmar din punct de vedere al prelucrărilor. 100% rezolvarea ei în Excel este doar un exercițiu de manipulare de date și rezultate, fără a avea pretenții de optimizare.

Problema MaxNonoverlappingSegments este o problemă clasică de optimizare care face parte din categoria Greedy algorithms (algoritmi lacomi). Aceasta constă în selectarea unui număr maxim de segmente (intervale) care nu se suprapun, dintr-un set de segmente date.

Avem o serie de segmente definite prin capete (start și end points), fiecare segment fiind reprezentat printr-o pereche de numere: (A[i],B[i]) unde:

• A[i] este punctul de început al segmentului.
• B[i] este punctul de sfârșit al segmentului.

Obiectivul este să alegem cât mai multe segmente care nu se suprapun, adică nu au puncte comune, astfel încât să maximizăm numărul total de segmente selectate.

O chichiță a problemei este dată de faptul că rezultatul final trebuie să fie prezentat în segmente de câte 3 și în combinații de câte 3 trebuie să prezentăm output-ul.

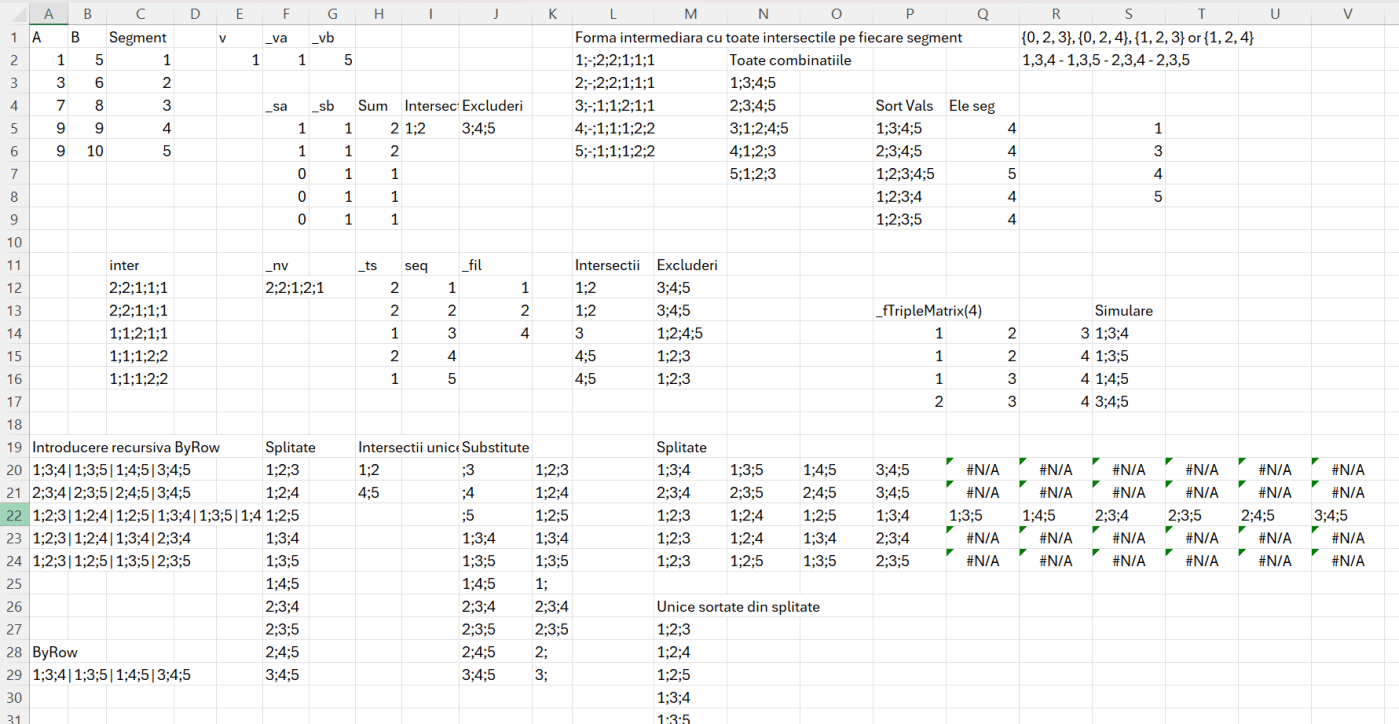
În imagine este prezentată rezolvarea graduală a problemei, proiecții intermediare pas cu pas, până a ajunge la forma finală din aproape în aproape.

Așa cum explicam în partea de teorie a acestui articol, cheia rezolvării constă în utilizarea funcției MAP și consțientizarea faptului că rezultatul trebuie să fie permanent o singură valoare.

Având în vedere că trebuie să returnăm valorile în seturi de câte 3 a trebuit să introduc și să salvez funcția _fTripleMatrix(elem) prezentată în aceste articole, care are următorul cod:

=LAMBDA(elem; LET(nrElemente; elem;
          combinatii; COMBIN(nrElemente; 3);
TripleG; SCAN("1;2;2"; SEQUENCE(combinatii);
   LAMBDA(a;v;
       LET(arr; --TEXTSPLIT(a;";");
           x; TAKE(arr;;1); y; TAKE(TAKE(arr;;2);;-1); z; TAKE(arr;;-1);
           newx; IF(AND(y=nrElemente-1; z=nrElemente);
                        IF(x<nrElemente-2; x+1; x); x);
           newy; IF(newx=x; IF(z=nrElemente;
                        IF(y<nrElemente-1; y+1; y);y); newx+1);
           newz; IF(newx=x; IF(z<nrElemente;z+1;y+2); newy+1);
newx&";"&newy&";"&newz)));
tabf; --TEXTSPLIT(TEXTJOIN("|";;TripleG);";";"|");
tabf))

în care elem este o valoare mai mare decât 3 și, așa cum explicam cu alte ocazii, poate avea un maxim de 189 pentru că numărul de combinații de 190 luate câte 3 depășește valoarea 2^20 care este numărul de linii dintr-o foaie de calcul Excel. Ca o curiozitate, în Google Spreadheet nu am reușit să generez o secvență de numere mai mare de 2^15.

Cheia rezolvării problemei este identificarea capetelor și intersecția lor cu alte segmente. Această secțiune este rezolvată în F5 și G5 printr-o funcție de mapare în care valoare 1 presupune intsecție cu alt interval, iar 0 lipsa intersecției. Dacă suma ambelor segmente se regăsește pe celălalt segment, atunci valoarea 2 ne spune că avem o intersecție. Valoarea 1 ne spune că acel segment nu se intersectează cu altul. Și de aici încep tot felul de calcule și filtre, mapări pe matricea de triplete dinamică și așa mai departe.

Formula finală integrată este:

=LET(_a;$A$2:$A$6;_b;$B$2:$B$6;segment;SEQUENCE(ROWS(_a));
      inter; MAP(segment;LAMBDA(v;LET(
                                   _va;INDEX(_a;v);
                                   _vb;INDEX(_b;v);
                                   _sa;MAP(_a;LAMBDA(_xa;_xa<=_vb));
                                   _sb;MAP(_b;LAMBDA(_xb;_xb>=_va));
                       tabi;BYROW(HSTACK(--_sa;--_sb);SUM);
                       TEXTJOIN(";";;tabi)
)));

    intersectii; MAP(inter; LAMBDA(_nv;
                      LET(_ts;--TEXTSPLIT(_nv;;";");seq;SEQUENCE(ROWS(_ts));
                           intersectii;TEXTJOIN(";";;FILTER(seq;_ts=2));
                           intersectii)));
    excluderi; MAP(inter; LAMBDA(_nv;
                      LET(_ts;--TEXTSPLIT(_nv;;";");seq;SEQUENCE(ROWS(_ts));
                          excluderi;TEXTJOIN(";";;FILTER(seq;_ts=1));
                          excluderi)));

    verif; HSTACK(VSTACK({"Segment"};segment);
                  VSTACK({"Intersectii"};intersectii);
                  VSTACK({"Excluderi"};excluderi);
                  VSTACK({"ArrayPoz"};segment-1));

    allExclude; BYROW(HSTACK(segment;excluderi); LAMBDA(r; TEXTJOIN(";";TRUE;r)));
    sorte; MAP(allExclude; LAMBDA(v; TEXTJOIN(";";;SORT(--TEXTSPLIT(v;;";")))));

   _freqBR; LAMBDA(x; LET(arr; --TEXTSPLIT(x;;";"); rr; ROWS(arr);
                          result; TEXTJOIN("|";;BYROW(_fTripleMatrix(rr); 
                                 LAMBDA(r; LET(_p1; TAKE(r; ;1); 
                                              _p2; INDEX(r; ;2); 
                                              _p3; TAKE(r; ;-1);
                                  TEXTJOIN(";";;INDEX(arr;_p1);INDEX(arr;_p2);INDEX(arr;_p3)))))); 
                          result));

    toatecomb; MAP(sorte; LAMBDA(v; _freqBR(v)));

    splitate; TEXTSPLIT(TEXTJOIN("-";;toatecomb);"|";"-");
    combunice; SORT(UNIQUE(TOCOL(splitate;3)));
    intersectiiUnice; FILTER(UNIQUE(intersectii); LEN(UNIQUE(intersectii))>1);

    checkIU; MAP(combunice; LAMBDA(v; LET(unice; intersectiiUnice; 
                                      IF(MIN(LEN(SUBSTITUTE(v; unice;"")))<5;FALSE;TRUE))));

   FILTER(combunice;checkIU)
)

O parte complexă din formulă este definirea funcției recursive _freqBR care înglobează funcția _fTripleMatrix() definită anterior. Am utilizat această tehnică pentru că în anumite moment anumite rezultate intermediare pot avea combinații diferite.

Cam atât pentru astăzi… Mai este o singură lecție pe site-ul Codility… dacă aveți alte colecții de probleme publice puteți să mi le oferiți în comentarii pentru a încerca abordarea lor. Eventual o resursă de probleme în română ar fi și mai fain.

Sper să fie util cuiva!